Matematiikan voidaan katsoa muodostuneen omaksi itsenäiseksi tieteekseen kreikkalaisen kulttuurin piirissä noin puoli vuosituhatta ennen ajanlaskumme alkua. Kreikkalaisen matematiikan ajanjakso ulottuu noin vuoteen 400 jKr. asti. Se voidaan karkeasti jakaa noin vuonna 300 eKr. päättyneeseen klassiseen kauteen ja sitä seuranneeseen hellenistiseen kauteen. Kun puhutaan antiikin Kreikan matematiikasta, ei maantieteellisesti rajoituta nykyiseen tai silloiseen Kreikkaan, vaan kysymys on paljon laajemmasta alueesta, joka käsitti myös Etelä-Italian, Sisilian, Vähän-Aasian ja Egyptin. Kaikki huomattavat matemaatikot eivät olleet kansallisuudeltaankaan kreikkalaisia.
Tiedot kreikkalaisen matematiikan varhaiskehityksestä perustuvat etupäässä lähes tuhat vuotta myöhemmin kirjoittaneen Prokluksen (410[?]-485 jKr.) historiaan. Myöhempienkään kreikkalaisten matemaatikkojen alkuperäisiä käsikirjoituksia ei ole säilynyt. Luultavasti monien tuntemiemme kreikkalaisten suurenmoisten matemaattisten saavutusten lisäksi paljon hienoa matematiikkaa on aikojen saatossa tuhoutunutkin. Hyvin suuri osa varhempien vuosisatojen kreikkalaisesta matematiikasta on koottu Eukleideen monumentaaliseen teokseen Alkeet, joka on kirjoitettu noin 300 eKr.
Kreikan perustavaa laatua oleva merkitys matematiikan historialle näkyy vaikkapa lukuisien matemaattisten termien kreikkalaisesta alkuperästä. Tällaisia ovat vaikkapa trigonometria, logaritmi, aritmetiikka, geometria, matematiikka, teoreema, tetraedri, probleema, ellipsi, paraabeli, hyperbeli, aksiooma, analyysi... Luetteloa voi jatkaa lähes rajatta.
Kauppaa käyvät kreikkalaiset kaupunkivaltiot tarvitsivat käytännön aritmetiikkaa. Erotukseksi lukujen ominaisuuksia tutkivasta ''oikeasta'' aritmetiikasta, nykytermein siis lukuteoriasta, käytännön laskemista kutsuttiin logistiikaksi.
Kreikkalaiset käyttivät lukujen merkinnässä kahta eri
järjestelmää. Vanhemmassa, attikalaisessa eli
herodiaanisessa järjestelmässä esitystapa oli samanlainen kuin
egyptiläisillä tai roomalaisilla, ts. ykkösellä, kymmenellä, sadalla,
tuhannella ja kymmenellätuhannella oli oma symbolinsa kullakin. (I=1,
![]() ,
ei iso gamma vaan vanha iso pi kuten pentagoni,
,
ei iso gamma vaan vanha iso pi kuten pentagoni, ![]() ,
H=100 - vrt. hehtaari - X=1000 - vrt. kilo - M=10000). Myöhemmässä,
joonialaisessa järjestelmässä kutakin
luvuista 1, 2,
,
H=100 - vrt. hehtaari - X=1000 - vrt. kilo - M=10000). Myöhemmässä,
joonialaisessa järjestelmässä kutakin
luvuista 1, 2, ![]() ,
9, 10, 20,
,
9, 10, 20, ![]() ,
90, 100, 200,
,
90, 100, 200, ![]() ,
900
vastasi aakkoston kirjain (1=A, 2=B,
,
900
vastasi aakkoston kirjain (1=A, 2=B, ![]() jne., myöhemmin
jne., myöhemmin
![]() jne.), lukuja 1000,
jne.), lukuja 1000, ![]() ,
9000 merkittiin vastaavilla ykkösten
symboleilla, joita edelsi pilkku, ja suurempia lukuja käyttämällä kerrointa
M = 104. Jotta luvut eivät sekoittuisi sanoihin, lukuja
tarkoittavien kirjainten tai kirjainyhdistelmien yläpuolelle vedettiin
vaakasuora viiva. Tavallisten kreikan aakkosten lisäksi numeromerkinnöissä
käytettiin muutamaa sittemmin aakkoskäytöstä poistunutta kirjainta.
- Vaikka kreikan kirjaimisto on paljolti lainaa foinikialaisilta, keksintö
käyttää kirjaimia numeroina on puhtaasti kreikkalainen.
,
9000 merkittiin vastaavilla ykkösten
symboleilla, joita edelsi pilkku, ja suurempia lukuja käyttämällä kerrointa
M = 104. Jotta luvut eivät sekoittuisi sanoihin, lukuja
tarkoittavien kirjainten tai kirjainyhdistelmien yläpuolelle vedettiin
vaakasuora viiva. Tavallisten kreikan aakkosten lisäksi numeromerkinnöissä
käytettiin muutamaa sittemmin aakkoskäytöstä poistunutta kirjainta.
- Vaikka kreikan kirjaimisto on paljolti lainaa foinikialaisilta, keksintö
käyttää kirjaimia numeroina on puhtaasti kreikkalainen.
Joonialainen numeromerkintä säilyi tieteellisessä käytössä länsimaissa vielä pitkään keskiajan lopulle, kauan nykyisen intialais-arabialaisen lukumerkinnän käyttööntulon jälkeenkin. - Joonialaiseen lukumerkintään ei varsinaisesti kuulunut murtolukuja; yksikkömurtoluvuista käytettiin kuitenkin merkintää, jossa nimittäjää esittävään symboliin liitettiin murtoluvun merkki, ja myöhemmin tulivat käyttöön seksagesimaalimurtoluvut (minuutit ja sekunnit).
Perimätiedon mukaan ensimmäinen nimeltä tunnettu kreikkalainen matemaatikko (ja matemaatikko yleensäkin) oli Vähän-Aasian Miletoksesta kotoisin ollut kauppias Thales (624[?]-547[?] eKr.). Thaleen, joka oli yksi Kreikan perinteen seitsemästä viisaasta, kerrottiin saaneen oppinsa Egyptistä. Hänen sanotaan esittäneen tai todistaneen seuraavat viisi geometrian teoreemaa. - Sanan teoreema, samoin kuin teorian ja teatterin pohjana on kreikan katsomista tarkoittava verbi.
Näistä erityisesti viimeinen kulkee edelleen nimellä Thaleen lause.
On huomattava perustavanlaatuinen ero Thaleen ja babylonialaisen tai egyptiläisen geometrian välillä: Thales muotoili yleispäteviä kuvioiden ominaisuuksia koskevia lauseita, jälkimmäiset esittivät laskennollisia ratkaisuja tiettyihin eksplisiittisesti muotoiltuihin probleemoihin. Epäselvempää on, mitä tarkoittaa, että Thales todisti nämä - ilmeisesti hän esitti väittämien tueksi rationaalisia perusteluja.
Noin puoli vuosisataa Thalesta nuorempi on Samos-saarelta kotoisin oleva
Pythagoras (572[?]-497 eKr.), niin ikään puoleksi
tarunomainen hahmo. Pythagoraan Etelä-Italian Crotoneen perustamalla
matemaattis-mystisellä koulukunnalla on ollut suuri merkitys matematiikan
kehitykselle itsenäiseksi tieteenalaksi. Sana ''matematiikka'',
![]() johdoksineen, lienee pythagoralaisten käyttöön
ottama, ja sen alkuperäinen merkitys on 'se, mikä tulee tietää'.
Pythagoralaisten keskuudessa sanotaan tulleen käyttöön opetussuunnitelman,
jossa geometrialla, aritmetiikalla, astronomialla ja
musiikilla, myöhemmin latinankielisellä nimellä quadrivium
tunnetulla yhdistelmällä, oli keskeinen asema. (Huom. Triviaali tulee
seitsemän vapaan taiteen oppijakson alkuosan humanistisemmista kolmesta
aineesta, grammatiikasta, retoriikasta ja logiikasta,
jotka muodostivat triviumin.)
johdoksineen, lienee pythagoralaisten käyttöön
ottama, ja sen alkuperäinen merkitys on 'se, mikä tulee tietää'.
Pythagoralaisten keskuudessa sanotaan tulleen käyttöön opetussuunnitelman,
jossa geometrialla, aritmetiikalla, astronomialla ja
musiikilla, myöhemmin latinankielisellä nimellä quadrivium
tunnetulla yhdistelmällä, oli keskeinen asema. (Huom. Triviaali tulee
seitsemän vapaan taiteen oppijakson alkuosan humanistisemmista kolmesta
aineesta, grammatiikasta, retoriikasta ja logiikasta,
jotka muodostivat triviumin.)
Pythagoralaisten veljeskunnan symboli oli viisikanta eli pentagrammi, säännöllisen viisikulmion lävistäjien muodostama viisisakarainen tähti, jonka keskustan muodostaa säännöllinen viisikulmio. Symbolin ja kuvioon sisältyvän matematiikan yhteydestä janojen yhteismitattomuuden keksimiseen on spekuloitu. Pythagoralaiset eivät juuri jättäneet kirjallisia lähteitä - veljeskunta siirsi tietoa suullisesti ja pyrki salaamaan oppinsa ulkopuolisilta. Turvallisempaa kuin liittää asioita suoraan Pythagoraaseen itseensä on sanoa niiden liittyvän pythagoralaisiin.
Keskeistä pythagoralaisten matematiikassa ja koko filosofiassa oli (luonnollinen) luku. Tässä mielessä Pythagoraan koulukuntaa voidaan pitää babylonialaisen aritmeettis-algebrallisen tradition jatkajana. Aritmetiikka erotettuna logistiikasta on pythagoralaista lähtöä. Pythagoralaisilta periytyvät paitsi lukumystiikkaan liittyvät käsitteet myös useat yhä käytössä olevat lukujen luokittelut. Tällainen on mm. luokittelu parilliset ja parittomat luvut. Yhtä ja toisinaan myös kahta ei pidetty samassa mielessä lukuina kuin nyt. Luokitusta tarkennettiin mm. jaolla pariton-pariton, pariton-parillinen, parillinen-parillinen. Luokittelu alkuluku - yhdistetty luku on myös pythagoralainen. Alkulukuja kutsuttiin lineaarisiksi luvuiksi, yhdistettyjä lukuja tasoluvuiksi. Jako täydellisiksi, vajaiksi ja abundanteiksi eli runsaiksi luvuiksi on myös vanha, joskaan sitä ei pystytä suoraan kytkemään pythagoralaisiin. Luku on vajaa, jos sen tekijöiden (1 mukana, luku itse ei) summa on pienempi kuin itse luku (1+2+4<8), täydellinen, jos summa on sama kuin luku (1+2+3=6) ja runsas, jos summa on suurempi kuin luku ( 1+2+4+6>12). Antiikin aikana tunnettiin neljä täydellistä lukua: 6, 28, 496 ja 8128. Lisäksi tiedettiin, että jos 2p-1 on alkuluku, niin 2p-1(2p-1) on täydellinen luku. - Euler todisti 1700-luvulla, että kaikki täydelliset luvut ovat tätä muotoa. Muotoa 2p-1 olevat alkuluvut ovat ns. Mersennen alkulukuja; usein uusien ja entistä tehokkaampien tietokoneiden testiajoissa saavutetut ''suurin tunnettu alkuluku'' -muotoiset ennätykset ovat poikkeuksetta koskeneet Mersennen alkulukuja.
Täydellisen luvun käsitteen sukulainen on ystävällisten lukujen käsite: n ja m ovat ystävällisiä, jos n on m:n tekijöiden summa ja m n:n tekijöiden summa. Pari m=284, n=220 on esimerkki tällaisista luvuista.
Tyypillinen pythagoralaisten tuote oli kuviolukujen
teoria. Kuviolukuja ovat kolmioluvut 1, 3, 5, ..., neliöluvut 1, 4, 9,
..., viisikulmioluvut 1, 5, 12, ... ja pitkänomaiset luvut
2, 6, 12, 20, .... Yleisesti 1. n-kulmioluku on 1, 2. on n. Jos k:nnetta
lukua ![]() edustaa n-kulmio ja siinä
olevat
edustaa n-kulmio ja siinä
olevat ![]() pistettä, k+1. saadaan jatkamalla kahta n-kulmion
sivua
pistettä, k+1. saadaan jatkamalla kahta n-kulmion
sivua
![]() -osalla pituudestaan, täydentämällä kuvio
n-kulmioksi ja lisäämällä uusille sivuille pisteitä niin, että
kuvion reunan joka sivulla on sama määrä pisteitä. Prosessissa
lisätyt pisteet
muodostavat gnomonin, kuvion, joka edustaa kahden peräkkäisen
kuvioluvun erotusta. Kuvioita, erityisesti gnomoneja tarkastelemalla näkee
helposti monia lukurelaatioita, mm.
-osalla pituudestaan, täydentämällä kuvio
n-kulmioksi ja lisäämällä uusille sivuille pisteitä niin, että
kuvion reunan joka sivulla on sama määrä pisteitä. Prosessissa
lisätyt pisteet
muodostavat gnomonin, kuvion, joka edustaa kahden peräkkäisen
kuvioluvun erotusta. Kuvioita, erityisesti gnomoneja tarkastelemalla näkee
helposti monia lukurelaatioita, mm.
Käsitteet aritmeettinen, geometrinen ja harmoninen
keskiarvo ovat peräisin pythagoralaisilta. Näihin johduttiin
ilmeisesti musiikkiin liittyvien numerosuhteiden tarkastelujen kautta,
pythagoralaiset kun havaitsivat, että jännitettyjen kielten
äänenkorkeudet ja kielten pituudet olivat tekemisissä toistensa kanssa.
Sen, että b on a:n ja c:n aritmeettinen, geometrinen tai harmoninen
keskiarvo voi karakterisoida yhtälöillä
Oktaavin päässä toisistaan olevia säveliä
vastaavien kielenpituuksien harmoninen keskiarvo antaa sävelen, joka on
kvinttiä korkeampi kuin alkuperäisistä sävelistä matalampi.
Sävelharmonia
teki lukukolmikon
![]() sinänsä harmoniseksi; seurauksena
oli esim., että kuutio, jossa on 6 sivutahkoa, 8 kärkeä ja 12
särmää, oli harmoninen kappale.
sinänsä harmoniseksi; seurauksena
oli esim., että kuutio, jossa on 6 sivutahkoa, 8 kärkeä ja 12
särmää, oli harmoninen kappale.
Pythagoralaiset määrittelivät a:lle ja c:lle kaikkiaan 10 eri keskiarvoa varioimalla a:n, b:n ja c:n paikkoja ylläolevan kaltaisissa kaavoissa.
Geometriassa riidattomimmin pythagoralaisiin liitettävä teoreema on kolmion kulmien summaa koskeva lause.
Pythagoraan lauseen alkuperä
kreikkalaisessa geometriassa on epäselvä. Olettamusta, jonka mukaan lause
tosiaan olisi peräisin itse Pythagoraalta, ei ainakaan voi helposti todistaa
vääräksi. Yksinkertainen ja mahdollisesti alkuperäinen lauseen todistus
hyödyntää yhdenmuotoisia kolmioita, jotka synnyttää hypotenuusaa vastaan
piirretty korkeus: jos x ja y ovat kateettien a ja b projektiot
hypotenuusalla c, niin
Pythagoralaisten kokonaislukuihin perustuva matematiikan järjestelmä johti ymmärrettävästi geometriassa yhteismitallisuuteen perustuvaan suhdeoppiin: geometrisia suureita yritettiin verrata toisiinsa niiden mittalukujen kautta. Pythagoralaisten järjestelmä koki melkoisen kriisin, kun (ilmeisesti viidennellä vuosisadalla ennen ajanlaskumme alkua kuitenkin Pythagoraan elinaikaa myöhemmin - vuosilukua 430 eKr. on esitetty) havaittiin, että monet yksinkertaiset janaparit, kuten neliön sivu ja lävistäjä tai jatkuvaan suhteeseen jaetun janan osat, eivät voi olla yhteismitallisia.
Tunnettu jaollisuuteen perustuva epäsuora todistus luvun ![]() irrationaalisuudelle (Jos
irrationaalisuudelle (Jos
![]() ja
ja
![]() on supistettu murtoluku, niin p2=2q2, joten p2 ja
siis p on parillinen, jolloin p2 ja siis 2q2 on jaollinen 4:llä,
ja q2 siis parillinen eli q parillinen,
mikä on ristiriidassa sen kanssa, että
on supistettu murtoluku, niin p2=2q2, joten p2 ja
siis p on parillinen, jolloin p2 ja siis 2q2 on jaollinen 4:llä,
ja q2 siis parillinen eli q parillinen,
mikä on ristiriidassa sen kanssa, että
![]() on supistettu.)
on mahdollisesti ollut
tuttu pythagoralaisille; ainakin Eukleides käyttää sitä.
Todistus yhdistettynä Pythagoraan
lauseeseen kertoo heti, että neliön sivu ja lävistäjä eivät
voi olla saman janan monikertoja: ne eivät siis ole yhteismitallisia.
on supistettu.)
on mahdollisesti ollut
tuttu pythagoralaisille; ainakin Eukleides käyttää sitä.
Todistus yhdistettynä Pythagoraan
lauseeseen kertoo heti, että neliön sivu ja lävistäjä eivät
voi olla saman janan monikertoja: ne eivät siis ole yhteismitallisia.
Toinen arveltu tie yhteismitattomien janojen olemassaolon
toteamiseen liittyy viisikantakuvioon. Jos viisikulmion sivu on a ja
lävistäjä d, on viisikantaan liittyviä tasakylkisiä kolmioita
tarkastelemalla melko helppo johtua tulokseen, jonka mukaan
![]() .
Viisikulmion sivu on
tämän mukaan pitempi niistä osista, jotka saadaan, kun lävistäjä
jaetaan ns.
jatkuvaan suhteeseen. Jatkuvaan suhteeseen perustuvaa jakoa voi jatkaa: jos
sivusta erotetaan lävistäjän jaon pienempi osa d-a, jäljelle
jääneen osan
a-(d-a)=2a-d suhde d-a:han on sama kuin d-a:n suhde a:han jne. Jos
nyt a ja d olisivat janan m monikertoja, olisi sitä d-a, 2a-d jne.,
mutta jakoja toistettaessa jako-osat pienenevät, ja lopulta alittavat m:n,
ja tullaan taas ristiriitaan. - Edellisissä päättelyissä on molemmissa
esiintynyt epäsuora todistus. Se on yksi kreikkalaisen matematiikan
ominaispiirteitä.
.
Viisikulmion sivu on
tämän mukaan pitempi niistä osista, jotka saadaan, kun lävistäjä
jaetaan ns.
jatkuvaan suhteeseen. Jatkuvaan suhteeseen perustuvaa jakoa voi jatkaa: jos
sivusta erotetaan lävistäjän jaon pienempi osa d-a, jäljelle
jääneen osan
a-(d-a)=2a-d suhde d-a:han on sama kuin d-a:n suhde a:han jne. Jos
nyt a ja d olisivat janan m monikertoja, olisi sitä d-a, 2a-d jne.,
mutta jakoja toistettaessa jako-osat pienenevät, ja lopulta alittavat m:n,
ja tullaan taas ristiriitaan. - Edellisissä päättelyissä on molemmissa
esiintynyt epäsuora todistus. Se on yksi kreikkalaisen matematiikan
ominaispiirteitä.
Yhteismitattomuuden havaitseminen ja tästä seuraava huomio, jonka mukaan pelkillä lukusuhteilla ei voida ilmaista geometrisia relaatioita, johti matematiikan painopisteen muuttumiseen geometrian suuntaan: aikaisemmin laskemalla ratkaistut tehtävät oli voitava ratkaista synteettisen geometrian keinoin, samaa ulottuvuutta olevien kuvioiden avulla. Huomattakoon, että kutsumme yhä x2:sta ja x3 x:n neliöksi ja kuutioksi.
Mm. toisen asteen yhtälöitä vastaavia tehtäviä ei
voinut ratkaista babylonialaisten tapaan laskualgoritmilla, vaan
laskualgoritmia vastaavalla geometrisella konstruktiolla. Tällainen
on ns. pinta-alan sovittaminen. Tehtävässä konstruoidaan
suorakaide, jonka kanta on annetun janan pituinen ja jonka ala ylittää
tai alittaa annetun
neliön alan neliöllä, jonka sivu on suorakaiteen korkeus. Algebrallisesti
tehtävä on
![]() .
Yksinkertainen geometrinen konstruktio tehtävän ratkaisemiseksi: piirretään
AB=a. Olkoon C AB:n keskipiste. Erotetaan AB:n keskinormaalilta
CO=b. Piirretään O-keskinen
.
Yksinkertainen geometrinen konstruktio tehtävän ratkaisemiseksi: piirretään
AB=a. Olkoon C AB:n keskipiste. Erotetaan AB:n keskinormaalilta
CO=b. Piirretään O-keskinen
![]() -säteinen ympyrä,
joka leikkaa puolisäteen CB pisteessä D. Nyt DB=x, sillä jos
piirretään neliö DBEF, niin suorakaiteen ADFG ala on
-säteinen ympyrä,
joka leikkaa puolisäteen CB pisteessä D. Nyt DB=x, sillä jos
piirretään neliö DBEF, niin suorakaiteen ADFG ala on
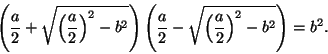
Tieteen historiaa sysäyksittäin etenevänä pitävät kutsuvat yhteismitattomuuden keksimistä matematiikan ensimmäiseksi suureksi kriisiksi.
Vanhin ilmeisesti jokseenkin alkuperäisen kaltaisena jälkimaailmalle säilynyt kreikkalainen matemaattinen teksti on Khiokselta kotoisin olleen Hippokrateen (joka on eri henkilö kuin lääketieteen isänä tunnettu Kosin Hippokrates) tasakylkiseen suorakulmaiseen kolmioon liittyvien ympyränkaarikaksikulmioiden eli Hippokrateen kuunsirppien pinta-alan määritys (noin 430 eKr.).
Puoliympyröiden, joiden halkaisijoina ovat (minkä hyvänsä)
suorakulmaisen kolmion hypotenuusa c ja kateetit a ja b, alat ovat
muotoa kc2, ka2 ja kb2, missä k on verrannollisuuskerroin (itse
asiassa
![]() ). Jos ison puoliympyrän ulkopuolelle
jäävien pienempien puoliympyröiden osien ala on X, niin koko kuvion ala
voidaan lausua kahdella tavalla:
). Jos ison puoliympyrän ulkopuolelle
jäävien pienempien puoliympyröiden osien ala on X, niin koko kuvion ala
voidaan lausua kahdella tavalla:
![]() .
Pythagoraan
lauseesta seuraa heti, että
.
Pythagoraan
lauseesta seuraa heti, että
![]() eli sama kuin suorakulmaisen
kolmion ala.
eli sama kuin suorakulmaisen
kolmion ala.
Hippokrateen sanotaan yrittäneen soveltaa samaa ideaa ympyrän
pinta-alan määrittämiseen seuraavasti: jos säännöllisen
kuusikulmion, jonka
sivu on r ja ala Y, ympäri piirretään ympyrä ja kunkin kuusikulmion
sivu
halkaisijana piirretään puoliympyrät, saadaan piparkakun muotoinen alue,
jonka ala on toisaalta
![]() ,
toisaalta
kr2+6X, missä X on ison ympyrän ja pienemmän puoliympyrän väliin
jäävän
alueen ala. Jos X tunnetaan, verrannollisuuskerroin k eli ympyrän ala
voidaan määrittää. Ongelmaksi muodostuu se, että X ei ole samoin
helposti
määritettävissä kuin vastaavassa suorakulmaisen kolmion tapauksessa. -
Trigonometrisin tarkasteluin voidaan osoittaa, että ympyränkaksikulmion
neliöinti onnistuu silloin ja vain silloin, kun kaksikulmiota rajoittavien
kaarien keskuskulmien suhde on jokin luvuista 2, 3,
,
toisaalta
kr2+6X, missä X on ison ympyrän ja pienemmän puoliympyrän väliin
jäävän
alueen ala. Jos X tunnetaan, verrannollisuuskerroin k eli ympyrän ala
voidaan määrittää. Ongelmaksi muodostuu se, että X ei ole samoin
helposti
määritettävissä kuin vastaavassa suorakulmaisen kolmion tapauksessa. -
Trigonometrisin tarkasteluin voidaan osoittaa, että ympyränkaksikulmion
neliöinti onnistuu silloin ja vain silloin, kun kaksikulmiota rajoittavien
kaarien keskuskulmien suhde on jokin luvuista 2, 3,
![]() ,
5,
,
5,
![]() .
Ensimmäinen, joka tämän todisti, oli Turun
Akatemian matematiikan professori
Martin Wallenius (1731-73).
.
Ensimmäinen, joka tämän todisti, oli Turun
Akatemian matematiikan professori
Martin Wallenius (1731-73).
Ympyrän pinta-alan määritys eli ympyrän neliöintiongelma on
yksi antiikin kolmesta suuresta matemaattisesta ongelmasta, joiden tutkimus
alkaa viidenneltä vuosisadalta eKr. Muut kaksi ovat kulman
kolmijako ja kuution kahdentaminen. Kaikissa tapauksissa ratkaisu
pyrittiin
saamaan puhtaasti geometrisin konstruktiomenetelmin, harpilla ja viivoittimella
eli ns.
euklidisilla työkaluilla. Vasta viime vuosisadalla kyettiin lopullisesti
osoittamaan, että mikään näistä konstruktioista ei onnistu.
Ympyrän neliöinnin mahdottomuus
palautuu siihen, että ![]() on transsendenttiluku (minkä todisti saksalainen
F. Lindeman (1852-1939) v. 1882), ja kulman kolmijaon sekä kuution
kahdentamisen
mahdottomuus siihen, että harppi ja viivoitinkonstruktioin voidaan tuottaa
vain pisteitä,
joiden koordinaatit saadaan lähtöpisteiden koordinaateista rationaalisin
laskutoimituksin
ja neliöjuuren otoin, kun taas mainitut ongelmat johtavat yleensä
kolmannen asteen
yhtälöihin, joille 1800-luvun alkupuolella kehittyneiden keinojen mukaan
tällainen
ratkaisu ei yleensä ole mahdollinen. Täsmällisen todistuksen kuution
kahdennustehtävän
ja kulman kolmijaon ratkeamattomuudelle harpilla ja viivoittimella antoi
ranskalainen
Pierre Wantzell (1814-48) vuonna 1837.
- Kolmijako-ongelma kiehtoo silti edelleen,
ja esim. yliopistojen matematiikan laitoksiin saapuu yhä ehdotuksia
ongelman ratkaisemiseksi.
on transsendenttiluku (minkä todisti saksalainen
F. Lindeman (1852-1939) v. 1882), ja kulman kolmijaon sekä kuution
kahdentamisen
mahdottomuus siihen, että harppi ja viivoitinkonstruktioin voidaan tuottaa
vain pisteitä,
joiden koordinaatit saadaan lähtöpisteiden koordinaateista rationaalisin
laskutoimituksin
ja neliöjuuren otoin, kun taas mainitut ongelmat johtavat yleensä
kolmannen asteen
yhtälöihin, joille 1800-luvun alkupuolella kehittyneiden keinojen mukaan
tällainen
ratkaisu ei yleensä ole mahdollinen. Täsmällisen todistuksen kuution
kahdennustehtävän
ja kulman kolmijaon ratkeamattomuudelle harpilla ja viivoittimella antoi
ranskalainen
Pierre Wantzell (1814-48) vuonna 1837.
- Kolmijako-ongelma kiehtoo silti edelleen,
ja esim. yliopistojen matematiikan laitoksiin saapuu yhä ehdotuksia
ongelman ratkaisemiseksi.
Antiikin kolme suurta ongelmaa ovat tyypillisiä puhtaan matematiikan ongelmia: niillä ei oikeastaan ole mitään tekemistä käytännön tarpeiden kanssa. Vaikka 2200 vuoden työ lopulta osoitti, että kaikki kolme ongelmaa ovat alkuperäisessä mielessä ratkeamattomia, niin ratkaisuyritysten vaatimien lisäapuneuvojen kehittely on monissa yhteyksissä vienyt matematiikan kehitystä eteenpäin: jo antiikissa esim. Menaikhmos (noin 350 eKr.) johtui kuutiota kahdentaessaan kartioleikkauskäyriin ja Hippias (noin 425 eKr.) kulman kolmijako-ongelman yhteydessä eräiseen transsendenttikäyrään.
Hippiaan käyrän, trisectrixin eli quadratrixin,
voi ajatella syntyvän
tasaisella kulmanopeudella pyörivän ympyrän säteen ja
tasaisella nopeudella liikkuvan, suuntansa säilyttävän janan leikkauspisteen
urana. Ajatellaan, että ympyrän keskipiste on origo ja säde kääntyy
vastapäivään niin, että sen toinen päätepiste lähtee pisteestä
![]() ja
päätyy pisteeseen
ja
päätyy pisteeseen ![]() .
Saman ajan kuluessa x-akselin suuntainen
jana puolestaan kohoaa niin, että sen toinen päätepiste siirtyy origosta
O pisteeseen B. Jos säteen ja janan leikkauspisteen piirtää
trisectrix-käyrän. Nykymerkinnöin käyrän yhtälöksi saataisiin
.
Saman ajan kuluessa x-akselin suuntainen
jana puolestaan kohoaa niin, että sen toinen päätepiste siirtyy origosta
O pisteeseen B. Jos säteen ja janan leikkauspisteen piirtää
trisectrix-käyrän. Nykymerkinnöin käyrän yhtälöksi saataisiin
Jos trisectrix on käytettävissä, kulman kolmijako (tai mihin
tahansa suhteeseen jako) on yksinkertaista. Sijoitetaan kulma, jonka suuruus
on ![]() niin, että sen kärki on origossa ja oikea kylki yhtyy
x-akseliin. Jos vasemman kyljen ja quadratrixin leikkauspiste on
niin, että sen kärki on origossa ja oikea kylki yhtyy
x-akseliin. Jos vasemman kyljen ja quadratrixin leikkauspiste on
![]() ,
niin suora
,
niin suora
![]() leikkaa
trisectrixin pisteessä P1 niin, että
leikkaa
trisectrixin pisteessä P1 niin, että
![]() .
Koska
.
Koska
Kolmijako-ongelmaan esitettiin myös mm. ns. neusis-ratkaisuja.
Niissä pyrittiin ''liu'uttamaan'' määrämittainen
jana asemaan, jota ei voi määrittää harpilla ja viivoittimella.
Arkhimedes
esitti sauraavan yksinkertaisen kolmijakokonstruktion: Olkoon annettu kulma
AOB, AO=OB=r. Piirretään O-keskinen r-säteinen ympyrä ja
piirretään
A:n kautta suora, joka leikkaa ympyrän myös pisteessä D ja suoran BOpisteessä C; asetetaan suora vielä niin, että CD=r (tämä on
neusis).
Tasakylkisistä kolmioista DCO ja DOA nähdään heti, että
![]() .
.
Kuution kahdennusongelma tunnettiin antiikin aikana myös Deloksen ongelmana. Legendan mukaan Delos-saarta vaivanneen kulkutautiepidemian vuoksi konsultoitu oraakkeli oli kehottanut kaksinkertaistamaan Apollon temppelin kuutionmuotoisen alttarin. Epidemia ei ollut hellittänyt, vaikka työmiehet olivat rakentaneet alttarin, jonka mittasuhteet olivat alkuperäiseen verraten kaksinkertaiset. Deloksen asukkaat kysyivät neuvoa Platonilta, jonka piirin matemaatikot yrittivät ratkaista ongelmaa.
Neliön kahdennustehtävä: etsi x, jolle x2=2a2, voidaan
ratkaista etsimällä a:n ja 2a:n keskiverto:
Hippokrates (joka eli paljon ennen Platonia!) keksi, että kuution
kahdennusongelma palautuu samalla tavoin kahden janan kahden keskiverron
määrittämiseen: jos
Menaikhmos puolestaan osoitti, että Hippokrateen versio ongelmasta palautui
paraabelin (nykyaikaisin merkinnöin esim.
![]() )
ja
hyperbelin (nykyaikaisin merkinnöin xy=a) leikkauspisteen etsimiseen.
)
ja
hyperbelin (nykyaikaisin merkinnöin xy=a) leikkauspisteen etsimiseen.
Yhteismitattomuuden tavoin merkittävää osaa kreikkalaisen
matematiikan kehityksessä näyttelivät elealaisen
Zenonin (n. 450
eKr.) liikettä, aikaa ja äärettömyyttä koskevat paradoksit
dikotomia, Akhilleus ja kilpikonna, nuoli ja
stadion. Jos on kuljettava 0:sta 1:een, on ohitettava pisteet
![]() ,
,
![]() ,
jne. äärettömän monessa pisteessä ei
voi vierailla äärellisessä ajassa, joten liike ei ole mahdollista.
Jotta Akhilleus tavoittaisi kilpikonnan, hänen on ensin päästävä
pisteeseen, jossa välimatka on puolet
alkuperäisestä, sitten pisteeseen, jossa se on neljäsosa
alkuperäisestä jne. Koska Akhilleuksen on ohitettava äärettömän monta
pistettä, hän ei ehdi koskaan tavoittaa kilpikonnaa. Lentävä nuoli on
jokaisena ajanhetkenä tietyssä paikassa. Se ei voi liikkua. Olkoon kolme
riviä esineitä:
,
jne. äärettömän monessa pisteessä ei
voi vierailla äärellisessä ajassa, joten liike ei ole mahdollista.
Jotta Akhilleus tavoittaisi kilpikonnan, hänen on ensin päästävä
pisteeseen, jossa välimatka on puolet
alkuperäisestä, sitten pisteeseen, jossa se on neljäsosa
alkuperäisestä jne. Koska Akhilleuksen on ohitettava äärettömän monta
pistettä, hän ei ehdi koskaan tavoittaa kilpikonnaa. Lentävä nuoli on
jokaisena ajanhetkenä tietyssä paikassa. Se ei voi liikkua. Olkoon kolme
riviä esineitä:
| A | A | A | A | ||
| B | B | B | B | ||
| C | C | C | C |
Jos A:t ovat paikallaan, B:t liikkuvat oikealle niin, että lyhyimpänä mahdollisena aikana B:t siirtyvät yhden pykälän A:ihin verrattuna ja C:t liikkuvat samoin vasemmalle, niin lyhyimpänä mahdollisena hetkenä B:t ja C:t siirtyvätkin toisiinsa nähden kaksi pykälää, joten on vielä lyhempiä hetkiä.
Zenonin paradoksit osoittavat, että avaruuden käsittäminen diskreetiksi - mikä oli kokonaislukuihin perustuvan pythagoralaisen matematiikan mukainen käsitys - johtaa ongelmiin. Aristoteles (384-322 eKr.) torjui paradoksit tuomalla matematiikkaan luvun ja suureen eron. Suuretta voidaan jakaa rajatta. Zenonin paradokseihin sisältyvät ongelmat tulivat uudelleen merkityksellisiksi nykyaikaisen matemaattisen analyysin myötä.
Vaikka filosofi Platon
(429-347 eKr.) ei itse ollut
matemaatikko, hänen Ateenassa toimineen filosofikoulunsa, Akademian,
(jonka portilla kerrotaan olleen tekstin
![]()
![]()
![]() ,
''pääsy
kielletty geometriaan perehtymättömiltä'') piirissä toimi useita
huomattavia
matemaatikkoja, mm. jo mainittu Menaikhmos. Platon itse oli ollut
kosketuksissa pythagoralaisiin Sisiliassa. Platonin
hahmotteleman ideaalivaltion filosofijohtajien tuli olla matemaattisesti
koulutettuja. Platonin omat filosofiset kirjoitukset ovat ensimmäisiä, joissa
esiintyy matematiikan perusteita käsitteleviä jaksoja. - Platonin
Valtio-teoksessa
esitetään, että sopivin valtion asukasmäärä on
,
''pääsy
kielletty geometriaan perehtymättömiltä'') piirissä toimi useita
huomattavia
matemaatikkoja, mm. jo mainittu Menaikhmos. Platon itse oli ollut
kosketuksissa pythagoralaisiin Sisiliassa. Platonin
hahmotteleman ideaalivaltion filosofijohtajien tuli olla matemaattisesti
koulutettuja. Platonin omat filosofiset kirjoitukset ovat ensimmäisiä, joissa
esiintyy matematiikan perusteita käsitteleviä jaksoja. - Platonin
Valtio-teoksessa
esitetään, että sopivin valtion asukasmäärä on
![]() ,
koska kyseinen luku on lukujen 12, 21 ja 20 tulo, koska sen
kahdestoista osa on jaollinen 12:lla ja koska se on jaollinen kaikilla
luvuilla 1:stä 12:een (paitsi 11:llä; kuitenkin 11 jakaa luvun 5
,
koska kyseinen luku on lukujen 12, 21 ja 20 tulo, koska sen
kahdestoista osa on jaollinen 12:lla ja koska se on jaollinen kaikilla
luvuilla 1:stä 12:een (paitsi 11:llä; kuitenkin 11 jakaa luvun 5![]() 038).
038).
Huomattavin Platonin piirin matemaattinen edustaja on knidoslainen
Eudoksos
(408[?]-355 eKr.), joka saattoi yhteismitattomien suureiden
suhdeopin loogisesti
pitävälle perustalle seuraavalla määrittelyllä: Jos A, B, C
ja D ovat samaa
laatua olevia suureita (pituuksia, pinta-aloja jne.), niin yhtäsuuruus
A : B = C : D on voimassa
silloin ja vain silloin, kun jokainen positiivisten kokonaislukujen pari
![]() toteuttaa tasan
yhden seuraavista kolmesta relaatiosta:
toteuttaa tasan
yhden seuraavista kolmesta relaatiosta:

Tämän voi tulkita vaikkapa niin, että kaksi ''irrationaalista'' suhdetta ovat samat, jos jokainen rationaalilukujen suhde, joka on toista irrationaalisuhdetta pienempi, on toistakin pienempi, mutta eri suuret, jos on olemassa rationaalilukusuhde, joka on toista irrationaalisuhdetta suurempi ja toista pienempi. Eudoksoksen määritelmä tulee hyvin lähelle runsaat kaksituhatta vuotta myöhemmin (1800-luvun lopulla) esitettyä reaaliluvun määrittelyä rationaalilukujen joukon ns. Dedekindin leikkauksena!
Toinen Eudoksoksen merkittävä keksintö oli ns. ekshaustio- eli tyhjennysmenetelmä pinta-alojen ja tilavuuksien määrittämiseksi tai yhtäsuuruuden todistamiseksi. Tyhjennysmenetelmän ydin on seuraava raja-arvokäsitteelle sukua oleva havainto: Olkoon annettuna kaksi suuretta, A ja B. Jos A:sta vähennetään suure, joka on suurempi kuin A/2, jäljellä olevasta osasta taas yli puolet jne., tullaan aina lopulta tilanteeseen, jossa jäännös on pienempi kuin B. Tyhjennysmenetelmän avulla voidaan muodostaa täsmällisiä epäsuoria todistuksia käyräviivaisia kuvioita koskeville lauseille ja määrittää pinta-aloja ja tilavuuksia, tarvitsematta varsinaisesti mennä raja-arvoihin tai vastaaviin äärettömiin prosesseihin.
Esimerkiksi lause ''ympyröiden alat suhtautuvat toisiinsa kuten
säteiden neliöt'' voidaan ekshaustiomenetelmällä todistaa epäsuorasti
vertaamalla ympyröiden aloja sisään piirrettyjen säännöllisten
monikulmioiden
aloihin, joiden tiedetään suhtautuvan kuten vastinjanojen neliöt.
Jos
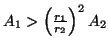 ja
ja
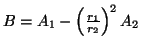 ,
saadaan jakoa tihentämällä
r1-säteisen ympyrän sisään piirretyn monikulmion ja alan ja A1:n
erotus pienemmäksi kuin B. Jos nimittäin k-kulmio vaihdetaan
2k-kulmioksi, ympyrän ja monikulmion välinen ala pienenee tasan
puolella sellaisten suorakaiteiden alasta, joiden kannat ovat k-kulmion
sivuja ja korkeudet monikulmion ja ympyrän erotuksen muodostavien
ympyränsegmenttien korkeuksia. Koska segmentin ala on pienempi kuin sitä
ympäröivän suorakaiteen, tyhjennysehto täyttyy. Jos nyt A1(k)
ja A2(k) ovat
ympyröiden sisään piirrettyjen säännöllisten k-kulmioiden alat,
niin jollain k:n arvolla
,
saadaan jakoa tihentämällä
r1-säteisen ympyrän sisään piirretyn monikulmion ja alan ja A1:n
erotus pienemmäksi kuin B. Jos nimittäin k-kulmio vaihdetaan
2k-kulmioksi, ympyrän ja monikulmion välinen ala pienenee tasan
puolella sellaisten suorakaiteiden alasta, joiden kannat ovat k-kulmion
sivuja ja korkeudet monikulmion ja ympyrän erotuksen muodostavien
ympyränsegmenttien korkeuksia. Koska segmentin ala on pienempi kuin sitä
ympäröivän suorakaiteen, tyhjennysehto täyttyy. Jos nyt A1(k)
ja A2(k) ovat
ympyröiden sisään piirrettyjen säännöllisten k-kulmioiden alat,
niin jollain k:n arvolla
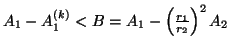 Tästä, monikulmioille tunnetusta tuloksesta
Tästä, monikulmioille tunnetusta tuloksesta
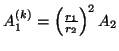 sekä epäyhtälöstä
A2(k)<A2, johdutaan ristiriitaan
sekä epäyhtälöstä
A2(k)<A2, johdutaan ristiriitaan
Toinen vastaavanlainen ristiriita johdetaan oletuksesta
A1 <(r1/r2)2A2.
Ainoaksi mahdollisuudeksi jää siis
![]() .
Eudoksoksen tyhjennysmenetelmäpäättelyjä voidaan pitää
integraalilaskennan edelläkävijänä. Tyhjennysmenetelmällä suoritetut
päättelyt ovat kuitenkin yleensä erittäin monimutkaisia. Kahden suureen
yhtäsuuruuden osoittaminen vaatii kaksi epäsuoraa todistusta, kummallekin
mahdolliselle epäyhtälön suuruussuunnalle. - Eudoksos oli paitsi
matemaatikko myös merkittävä tähtitieteilijä. Hänen
hahmottelemansa maailmanjärjestys perustui 27:ään sisäkkäiseen eri
tavoin
pyörivään palloon, joiden yhteisvaikutuksena syntyvä taivaankappaleiden
liike oli kohtuullisen hyvin sopusoinnussa havaintojen kanssa.
.
Eudoksoksen tyhjennysmenetelmäpäättelyjä voidaan pitää
integraalilaskennan edelläkävijänä. Tyhjennysmenetelmällä suoritetut
päättelyt ovat kuitenkin yleensä erittäin monimutkaisia. Kahden suureen
yhtäsuuruuden osoittaminen vaatii kaksi epäsuoraa todistusta, kummallekin
mahdolliselle epäyhtälön suuruussuunnalle. - Eudoksos oli paitsi
matemaatikko myös merkittävä tähtitieteilijä. Hänen
hahmottelemansa maailmanjärjestys perustui 27:ään sisäkkäiseen eri
tavoin
pyörivään palloon, joiden yhteisvaikutuksena syntyvä taivaankappaleiden
liike oli kohtuullisen hyvin sopusoinnussa havaintojen kanssa.
Aleksanteri Suuren seuraaja Egyptissä, Ptolemaios I, perusti noin 300 eKr. Aleksandriaan Museion-nimisen instituutin, ota voidaan pitää maailman ensimmäisenä yliopistona. Museionin ensimmäinen matematiikan edustaja oli Eukleides (365[?]-300[?] eKr.). Eukleideen kuuluisin teos on Stoikheia, eli Alkeet, joka tunnetaan yleisesti myös latinankielisellä nimellään Elementa. Alkeet on luultavasti kaikkien aikojen menestyksellisin matemaattis-luonnontieteellinen teos. Se levisi lukemattomina käsikirjoituksina (joissa luonnollisesti oli virheitä ja parannuksia tai parannusyrityksiä) ja käännöksinä; vuodesta 1482 alkaen on myös painettuja versioita ainakin toista tuhatta. Kouluopetuksessa teos oli keskeisenä oppikirjana viime vuosisadalle asti useissa maissa, myös Suomessa. - Samanlaisia yleisesityksiä oli kyllä kirjoitettu jo ennen Eukleidesta. Mm. Hippokrateen tuotantoon tiedetään kuuluneen Alkeet-teoksen, joka kuitenkaan ei ole säilynyt.
Alkeet sisältää 13 ''kirjassa'' ja 465 propositiossa koko Eukleidesta
edeltävän ajan matematiikan yleisesityksen. Suuri osa teoksen
sisällöstä on
peräisin Eukleideen edeltäjiltä. Paitsi alkeisgeometrian aksiomaattista
käsittelyä teos sisältää mm. Eudoksoksen suhdeopin ja
ekshaustiomenetelmän, koko joukon alkuaan pythagoralaista
lukuteoriaa, esim. Eukleideen algoritmin kahden luvun
suurimman yhteisen tekijän
tai kahden suureen yhteisen mitan löytämiseksi. Lukujen a ja b yhteiset
tekijät ovat tekijöinä jakoyhtälön
a=q1b+r1 mukaisessa
jakojäännöksessä
r1, jakoyhtälön
b=q2r1+r2 jakojäännöksessä r2 jne. Koska
![]() ,
jokin jakojäännös on viimeinen positiivinen
jakojäännös.
Siinä ovat edelleen tekijöinä a:n ja b:n yhteiset tekijät ja vain
ne. Jos
a ja b ovat mielivaltaisia suureita, esim. janoja, Eukleideen algoritmi
päättyy äärellisen monen askeleen jälkeen, jos ja vain jos a ja
b ovat yhteismitallisia.
,
jokin jakojäännös on viimeinen positiivinen
jakojäännös.
Siinä ovat edelleen tekijöinä a:n ja b:n yhteiset tekijät ja vain
ne. Jos
a ja b ovat mielivaltaisia suureita, esim. janoja, Eukleideen algoritmi
päättyy äärellisen monen askeleen jälkeen, jos ja vain jos a ja
b ovat yhteismitallisia.
Klassisen kaunis todistus alkulukujen määrän rajattomuudesta
saattaa olla Eukleideen oma oivallus. Mitä hyvänsä äärellistä
alkulukujen kokoelmaa
![]() kohden voidaan valita luku,
jossa ne kaikki ovat tekijöinä, esim. lukujen tulo
kohden voidaan valita luku,
jossa ne kaikki ovat tekijöinä, esim. lukujen tulo
![]() ,
ja
lisätä tätä lukua yhdellä. Luku
,
ja
lisätä tätä lukua yhdellä. Luku
![]() on joko itse
alkuluku tai sillä on alkutekijä, joka ei voi olla mikään luvuista
p1, p2, ...pk.
on joko itse
alkuluku tai sillä on alkutekijä, joka ei voi olla mikään luvuista
p1, p2, ...pk.
Stoikheian kirjoista laajin on kirja X, joka sisältää muotoa
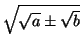 olevien suureiden luokittelun. Viimeiset kirjat
käsittelevät avaruusgeometriaa ja huipentuvat todistukseen täsmälleen
viiden säännöllisen monitahokkaan (''Platonin
kappaleen'') olemassaolosta ja näiden kappaleiden tilavuuksien laskemiseen.
olevien suureiden luokittelun. Viimeiset kirjat
käsittelevät avaruusgeometriaa ja huipentuvat todistukseen täsmälleen
viiden säännöllisen monitahokkaan (''Platonin
kappaleen'') olemassaolosta ja näiden kappaleiden tilavuuksien laskemiseen.
Stoikheian merkitys on paitsi sisällössä myös esitystavassa. Teos alkaa joukosta määritelmiä, aksioomia ja postulaatteja, jotka oletetaan annetuiksi. Aksioomalla ymmärrettiin yleispätevää, kaikkiin oppeihin sovellettavissa olevaa totuutta (''kokonainen on osaansa suurempi''), postulaatilla puolestaan käsiteltävälle opille erityisiä perustotuuksia. Kaikki muut lauseet johdetaan suoraan tai välillisesti näistä. Yleisenä tiedonmuodostusmenetelmänä aksiomattis-deduktiivinen metodi on lähtöisin Aristoteleelta. Myöhemmin on Eukleideen päättelyistä löydetty sieltä täältä aukkoja ja virheitä, mutta itse aksiomaattis-deduktiivinen metodi on tullut matematiikan vakiintuneeksi esitystavaksi. - Eukleideen kolme ensimmäistä postulaattia koskevat mahdollisuutta piirtää suora kahden pisteen kautta, mahdollisuutta jatkaa suoraa rajatta kumpaankin suuntaan ja mahdollisuutta piirtää ympyrä, jonka keskipiste ja säde ovat annetut. Postulaatit määrittelevät nämä konstruktiot yksikäsitteisiksi. Neljäs postulaatti sanoo kaikkien suorien kulmien olevan yhteneviä.
Eukleideen viides postulaatti on ns. paralleeliaksiooma, jonka itsestäänselvyys ei ole läheskään niin kiistaton kuin muiden postulaattien.
Jos suora leikkaa kaksi muuta suoraa niin, että samalla puolella suoraa olevien kahden sisäkulman summa on pienempi kuin kaksi suoraa kulmaa, niin mainitut kaksi suoraa leikkaavat toisensa sillä puolen ensimmäistä suoraa, missä kulmien summa on vähemmän kuin kaksi suoraa kulmaa.Monet matemaatikot yrittivät eri aikoina johtaa paralleelipostulaatin muista aksioomista. Vasta 1800-luvulla nämä yritykset osoitettiin mahdottomiksi, samalla kun konstruoitiin ns. epäeuklidisia geometrioita, joissa paralleelipostulaatin korvaa jokin muu suorien yhdensuuntaisuutta koskeva oletus.
Antiikin lahjakkaimpana matemaatikkona ja luonnontieteilijänä pidetään Arkhimedesta (287[?]-212 eKr.). Hän toimi Syrakusassa, mutta oli ilmeisesti saanut koulutuksensa Aleksandriassa. Useimmat Arkhimedeen teknistä taitavuutta koskevat kertomukset liittyvät Syrakusan piiritykseen ja valloitukseen Rooman ja Karthagon välisessä toisessa puunilaissodassa. Vaikka Arkhimedeen kuuluisuus liittyy ennen muuta hänen fysikaalis-teknisiin keksintöihinsä, tarina Arkhimedeen kuolemasta kertoo hänen askarrelleen matematiikan parissa silloinkin, kun roomalainen sotilas hänet surmasi. Arkhimedeen väitetyt viimeiset sanat ''älä sotke ympyröitäni'', ''noli turbare circulos meos'' ovat jääneet lentäväksi lauseeksi. Arkhimedes oli ensimmäinen rationaalisia fysikaalisia periaatteita kehitellyt ajattelija: hänen keksintöään ovat vipulaki (''antakaa minulle kiinteä piste, niin vipuan maan paikoiltaan'') ja hydrostatiikan Arkhimedeen periaate (kappaleeseen kohdistuva noste on yhtä suuri kuin kappaleen syrjäyttämän nestemäärän paino). Tunnettu Arkhimedes-legenda kertoo Arkhimedeen heureka-huudahduksesta hänen oivallettuaan nostelain.
Arkhimedeen monipuolisen matemaattisen tuotannon painopiste on
aiheissa, jotka nykyisin katsotaan integraalilaskennaksi: hän todisti
täsmällisesti, ekshaustiomenetelmää käyttäen, että ympyrän ala
on puolet
säteen ja kehän tulosta, laski paraabelin segmentin ja ellipsin alan, pallon
alan ja tilavuuden, pyörähdyskappaleiden tilavuuksia, erilaisten kuvioiden ja
kappaleiden painopisteitä, ympyrän kehän pituuden likiarvoja kuten
säännöllisen 96-kulmion ominaisuuksista johdettavan
Arkhimedeen säilyneissä kirjoituksissa esiintyvät todistukset perustuvat vaikean ekshaustiomenetelmän käyttöön. Vuonna 1906 löydettiin kuitenkin Arkhimedeen aleksandrialaiselle Eratostheneelle (n. 276 - n. 196 eKr.; tunnettu mm. alkuluvut tuottavasta Eratostheneen seulasta ja maapallon mittasuhteiden rationaalisesta määrittämisestä) kirjoittama kirje, joka tunnetaan nimellä Metodi. Siinä esitetään oikotie: alue, jonka pinta-ala halutaan laskea, jaetaan janoiksi, joita verrataan pinta-alaltaan tunnetun alueen janoihin asettamalla kyseiset osat ikään kuin erivartisen vaa'an kuppeihin. Tällä integraalilaskentaa muistuttavalla menetelmällä Arkhimedes pystyi nopeasti laskemaan esim. paraabelinkaaren rajoittamien alueiden aloja, mutta koska menetelmä oli loogisesti epätyydyttävä (äärettömän monen äärettömän pienen suureen summat!), hän varmensi tulokset ekshaustiomenetelmään perustuvin todistuksin.
Arkhimedeen punnitusideaa voi tarkastella esim. seuraavassa hiukan
nykyaikaistetussa esimerkissä: halutaan laskea
Paraabelin alan laskemista ekshaustiomenetelmällä voi edustaa
seuraava nykymerkinnöin esitetty Arkhimedeen päättely. Lasketaan suorien
y=1 ja x=0 paraabelista y=x2 erottama ala S. Se voidaan tyhjentää
kolmioilla ![]() ,
jonka kärjet ovat
,
jonka kärjet ovat ![]() ,
,
![]() ja
ja ![]() ,
,
![]() ,
jonka kärjet ovat
,
jonka kärjet ovat ![]() ,
,
![]() ja
ja ![]() ,
,
![]() ja
ja
![]() ,
joiden kärjet ovat
,
joiden kärjet ovat ![]() ,
,
![]() ja
ja
![]() sekä
sekä
![]() ,
,
![]() ja
ja ![]() jne. Kolmion
jne. Kolmion
![]() ala on
ala on
![]() .
Suora
.
Suora
![]() jakaa kolmion
jakaa kolmion
![]() kahdeksi kolmioksi, joilla on yhteinen kanta,
jonka pituus on
kahdeksi kolmioksi, joilla on yhteinen kanta,
jonka pituus on
![]() ja yhteinen korkeus
ja yhteinen korkeus
![]() .
Kummankin kolmion ala on näin ollen
.
Kummankin kolmion ala on näin ollen
![]() ,
joten kolmion
,
joten kolmion ![]() ala on
ala on
![]() .
Samoin nähdään, että kolmioiden
.
Samoin nähdään, että kolmioiden
![]() ja
ja
![]() yhteinen ala on
yhteinen ala on
![]() .
n:n vaiheen
jälkeen kolmioiden ala on
.
n:n vaiheen
jälkeen kolmioiden ala on
![]() .
Joka vaiheessa uudet kolmiot peittävät yli puolet edellisten kolmioiden
ja paraabelin väliin jäävästä alueesta. Oletukset
.
Joka vaiheessa uudet kolmiot peittävät yli puolet edellisten kolmioiden
ja paraabelin väliin jäävästä alueesta. Oletukset
![]() ja
ja
![]() johtavat ristiriitaan. (Arkhimedeella oli käytössään
jo Eukleideen tuntema kaava päättyvän geometrisen sarjan summalle.) Siis
johtavat ristiriitaan. (Arkhimedeella oli käytössään
jo Eukleideen tuntema kaava päättyvän geometrisen sarjan summalle.) Siis
![]() .
.
Arkhimedeen spiraali on transsendenttikäyrä, jonka muodostaa
tasaisella nopeudella pyörivällä säteellä tasaisella nopeudella
liikkuva piste. Arkhimedeen spiraalin napakoordinaattimuotoinen yhtälö on
![]() .
Arkhimedes määritti sekä spiraalin tangentin pituuden että
spiraalin ja radiusvektoreiden rajoittaman alueen pinta-alan.
.
Arkhimedes määritti sekä spiraalin tangentin pituuden että
spiraalin ja radiusvektoreiden rajoittaman alueen pinta-alan.
Arkhimedeelle itselleen oli erityisen läheinen pallon tilavuuden
johto; hän toivoi hautakiveensä kuvion, joka esittää palloa, kartiota ja
lieriötä. Jos r-säteinen pallo sijoitetaan r-säteisen ja
2r-korkeuksisen lieriön sisään ja samaan kuvioon liitetään kartio,
jonka huippu on pallon keskipisteessä ja jonka pohja yhtyy lieriön pohjaan,
niin etäisyydellä x pallon keskipisteestä tehty lieriön ja kartion
akselia
vastaan kohtisuora tasoleikkaus erottaa lieriöstä r-säteisen ympyrän,
pallosta
![]() -säteisen ympyrän ja kartiosta x-säteisen
ympyrän. Koska ympyrän ala on verrannollinen ympyrän säteeseen, pallon ja
kartion ympyräleikkausten yhteinen ala on
-säteisen ympyrän ja kartiosta x-säteisen
ympyrän. Koska ympyrän ala on verrannollinen ympyrän säteeseen, pallon ja
kartion ympyräleikkausten yhteinen ala on
![]() .
Koska pallon ja kartion leikkaukset näin tasapainottavat lieriön leikkaukset,
on puolipallon ja kartion yhteinen tilavuus sama kuin lieriön(puolikkaan).
Tästä seuraa, että pallon tilavuus on
.
Koska pallon ja kartion leikkaukset näin tasapainottavat lieriön leikkaukset,
on puolipallon ja kartion yhteinen tilavuus sama kuin lieriön(puolikkaan).
Tästä seuraa, että pallon tilavuus on
![]() lieriön
tilavuudesta (joka on pohjaympyrän ala kerrottuna korkeudella). Pallon
tilavuuden määritys palautuu täten ympyrän neliöintiongelmaan.
lieriön
tilavuudesta (joka on pohjaympyrän ala kerrottuna korkeudella). Pallon
tilavuuden määritys palautuu täten ympyrän neliöintiongelmaan.
Eräs Arkhimedeen saavutuksia oli erittäin suurten lukujen
merkitsemiseen soveltuva lukujen merkintätapa (jota Arkhimedes demonstroi
mielikuvituksellisella laskutehtävällä: laskemalla maailmankaikkeuden
täyttämiseksi tarvittavien hiekanjyvästen määrän - Arkhimedeen
mukaan 1063). Tässä yhteydessä Arkhimedes johtui
lähelle logaritmilaskennan perusperiaatetta, lukujen kertolaskua vastaa
eksponenttien yhteenlasku. Arkhimedes totesi, että luvut 1:stä 108:aan eli
myriadi myriadiin asti ovat nimettävissä, Ne muodostavat ensimmäisen
luokan, luvut 108:sta 1016:een muodostavat toisen luokan jne.,
kunnes
![]() päättää ensimmäisen jakson.
Toisen jakson suurin luku on P2;
menetelmää jatketaan, kunnes tullaan P:nteen jaksoon, jonka suurin luku on
P108. Arkhimedeen järjestelmä mahdollistaisi kaikkien
kymmenjärjestelmässä enintään 80000 biljoonalla numerolla kirjoitettavien
lukujen nimeämisen. - Arkhimedeen nimissä on myös ns. karjaongelma,
hiukan epäselvästi muotoiltu kokonaislukuyhtälöryhmä, joka tavallisen
tulkinnan mukaan redusoituu yhtälöön
x2-4729494y2=1. Yhtälön
ratkaisut
ovat niin suuria lukuja, että niiden kirjoittamiseen tarvittaisiin
satojatuhansia numeroita.
päättää ensimmäisen jakson.
Toisen jakson suurin luku on P2;
menetelmää jatketaan, kunnes tullaan P:nteen jaksoon, jonka suurin luku on
P108. Arkhimedeen järjestelmä mahdollistaisi kaikkien
kymmenjärjestelmässä enintään 80000 biljoonalla numerolla kirjoitettavien
lukujen nimeämisen. - Arkhimedeen nimissä on myös ns. karjaongelma,
hiukan epäselvästi muotoiltu kokonaislukuyhtälöryhmä, joka tavallisen
tulkinnan mukaan redusoituu yhtälöön
x2-4729494y2=1. Yhtälön
ratkaisut
ovat niin suuria lukuja, että niiden kirjoittamiseen tarvittaisiin
satojatuhansia numeroita.
Menaikhmoksen aloittaman kartioleikkauskäyrien teorian
tutkimuksen vei pisimmälle pergalainen, Aleksandriassa opiskellut
Apollonios (260[?]-170 eKr.), jonka kahdeksanosainen
kartioleikkausten teorian yleisesitys Conica sisältää
aiheesta olennaisesti samat tiedot kuin vakiintunut analyyttisen geometrian
oppimäärä nykyisin: kartioleikkausten halkaisijat, tangentit,
normaalit, leikkaaminen, asymptootit. Esitys on kuitenkin puhtaasti
synteettisen geometrian mukainen, koordinaatteja tai muita laskennallisia
apuneuvoja Apollonios ei sallinut tai tuntenut. Tutut nimitykset
ellipsi, paraabeli ja hyperbeli ovat peräisin
Apolloniokselta; ne voidaan nykyaikaisia merkintöjä käyttäen
ymmärtää vertaamalla paraabelin (''asettaa rinnalle'') yhtälöä
Alkuaan kartioleikkaukset ajateltiin aina syntyviksi suorista ympyräkartioista sivuviivoja vastaan kohtisuorilla tasoilla tehdyissä leikkauksissa. Ellipsi, paraabeli ja hyperbeli olivat siten terävä-, suora- ja tylppäkulmaisen kartion leikkauksia. Apollonios käytti yleistä kartiota ja leikkaustasoa.
Olkoon A ympyräpohjaisen kartion kärki ja BC pohjaympyrän
halkaisija. Leikataan kartio tasolla ![]() ,
joka ei ole pohjatason
suuntainen ja joka leikkaa suoran BC pisteessä T, joka ei ole janalla
BC, sekä suorat AB ja AC pisteissä Q ja R. Olkoon Pmielivaltainen tason
,
joka ei ole pohjatason
suuntainen ja joka leikkaa suoran BC pisteessä T, joka ei ole janalla
BC, sekä suorat AB ja AC pisteissä Q ja R. Olkoon Pmielivaltainen tason ![]() ja kartiopinnan leikkauskäyrän piste ja
leikatkoon P:n kautta piirretty QR:ää vastaan kohtisuora suora QR:n
pisteessä H ja kartiopinnan vielä pisteessä P'. Asetetaan nyt suoran
PP' kautta pohjaympyrän suntainen taso, joka leikkaa kartiopinnan pitkin
ympyrää ja suorat AB ja AC pisteissä D ja E. Yhdenmuotoisista
kolmioista saadaan heti
ja kartiopinnan leikkauskäyrän piste ja
leikatkoon P:n kautta piirretty QR:ää vastaan kohtisuora suora QR:n
pisteessä H ja kartiopinnan vielä pisteessä P'. Asetetaan nyt suoran
PP' kautta pohjaympyrän suntainen taso, joka leikkaa kartiopinnan pitkin
ympyrää ja suorat AB ja AC pisteissä D ja E. Yhdenmuotoisista
kolmioista saadaan heti
Kartioleikkausten teorian kehittyminen lähes 2000 vuotta ennen kuin niiden fysikaalinen merkitys tuli ilmi Keplerin planeettateorian ja Newtonin mekaniikan myötä on yksi vastaesimerkki teoreettisen, ''puhtaan'' matematiikan hyödyllisyyttä epäileville.
Kreikkalaisen antiikin merkittävin aritmeettis-algebrallisen perinteen edustaja oli aleksandrialainen Diofantos (250 jKr.?). Hänen pääteoksensa Arithmetika sisältää suuren ja monipuolisen joukon yhden tai useamman tuntemattoman ensimmäisen ja toisen asteen yhtälöiksi tunnistettavia probleemoja, joihin etsitään kokonaislukuratkaisuja; näitä yhtälöitä kutsutaan nykyäänkin Diofantoksen yhtälöiksi.
Diofantoksen ratkaisut perustuvat yleensä kekseliäisiin
oivalluksiin eivätkä ne muodosta yhtenäistä teoriaa. Diofantos on
ensimmäinen
kirjoittaja, jonka teksteissä esiintyy algebrallisen symbolismin alkeita.
Diofantoksen symboliikka soveltui polynomilausekkeiden kirjoittamiseen.
Hän käytti
tuntemattomalle lyhennysmerkintää, jonka tarkka muoto on kopioinneissa
hämärtynyt, mutta jonka on arveltu syntyneen sanan
![]() ensimmäisistä kirjaimista
ensimmäisistä kirjaimista
![]() .
Merkintä muistuttaa
kirjainta
.
Merkintä muistuttaa
kirjainta ![]() .
Tuntemattoman toista potenssia Diofantos merkitsi
.
Tuntemattoman toista potenssia Diofantos merkitsi
![]() ja sen kolmatta potenssia
ja sen kolmatta potenssia
![]() .
Neljäs,
viides ja kuudes potenssi olivat
.
Neljäs,
viides ja kuudes potenssi olivat
![]() ,
,
![]() ja
ja
![]() .
Vakiotermin merkki oli
.
Vakiotermin merkki oli
![]() .
Symbolia seurasi tuntemattoman
kertoimen numeroarvo (joonialaisin numeroin), ja yhteenlasku osoitettiin
kirjoittamalla termit perätysten. Matemaattisista operaattoreista
vain vähennyslaskun operaattorille oli
Diofantoksen järjestelmässä oma merkkinsä.
Se oli
.
Symbolia seurasi tuntemattoman
kertoimen numeroarvo (joonialaisin numeroin), ja yhteenlasku osoitettiin
kirjoittamalla termit perätysten. Matemaattisista operaattoreista
vain vähennyslaskun operaattorille oli
Diofantoksen järjestelmässä oma merkkinsä.
Se oli
![]()
![]() ,
joka edelsi vähennettäviä termejä. Merkintä
,
joka edelsi vähennettäviä termejä. Merkintä
![]() tarkoittaisi polynomia
2x3+5x-3x2-44.
tarkoittaisi polynomia
2x3+5x-3x2-44.
Suurin osa Diofantoksen Arithmetikan ongelmista koskee yhden tai useamman tuntemattoman polynomiyhtälöitä, kuten y2=Ax2+Bx+C tai y2=Ax3+Bx2+Cx+D. Yhtälöt ovat joko determinoituja tai ei. Kertoimet on yleensä valittu niin, että sopivien sijoitusten jälkeen jäljelle jää lineaarinen yhtälö. Esimerkiksi yhtälö y2=Ax2+Bx+C voidaan ratkaista, jos A=a2 tai C=c2. Edellisessä tapauksessa sijoitus y=ax+m johtaa yhtälöön 2amx+m2=Bx+C, jälkimmäisessä tapauksessa sijoitus y=mx+cyhtälöön m2x2+2mx=Ax2+Bx eli (m2-A)x=B-2m. Pythagoraan lukuihin johtavan tehtävän x2+y2=a2 Diofantos ratkaisi sijoituksella y=mx-a. Diofantos hyväksyi vain rationaaliset juuret ja aina vain yhden juuren.
Tarinan mukaan Diofantoksen iän voi laskea seuraavien tietojen perusteella:
Diofantos eli:n elämästään lapsena,
:n nuorukaisena ja sitten vielä
:n poikamiehenä. Viisi vuotta sen jälkeen, kun Diofantos oli nemmyt naimisiin, hän sai pojan, joka kuoli neljä vuotta isäänsä ennen ja saavutti puolet isänsä ikävuosista.
Nykyisin trigonometriaksi kutsuttavan opin ensi vaiheet
sattuvat hellenistiselle kaudelle. Tähtitieteilijät
Hipparkhos (180[?]-125 eKr.) ja
Klaudios Ptolemaios
(85[?]-165 jKr.), nerokkaan joskin virheellisen
maakeskisen maailmanjärjestyksen esittäjä, laativat taulukoita eri
keskuskulmia vastaavien jänteiden pituuksista, siis trigonometrian
taulukoiden edeltäjiä. Ptolemaioksen Syntaxis Mathematica-
ja Almagest-nimillä tunnettuun pääteokseen sisältyy
trigonometristen
taulukoiden laatimisperusteiden kuvaus. Ptolemaios laski taulukkoarvot
''helppojen'' kulmien perusteella käyttäen apuna lauseita, joka mahdollistivat
puolta kulmaa ja kahden kulman summaa vastaavien jänteiden laskemisen.
Tällainen on Ptolemaioksen lause, jonka mukaan jännenelikulmion
ABCD janoille pätee
![]() .
Lause on helppo todistaa valitsemalla
AC:n piste E, jolle
.
Lause on helppo todistaa valitsemalla
AC:n piste E, jolle
![]() ;
silloin kolmiot ABE ja
DBC sekä ABD ja ECB ovat keskenään yhdenmuotoisia.
Yhdenmuotoisuuksista
seuraa
;
silloin kolmiot ABE ja
DBC sekä ABD ja ECB ovat keskenään yhdenmuotoisia.
Yhdenmuotoisuuksista
seuraa
![]() ja
ja
![]() ja edelleen
ja edelleen
![]() .
Tarkastelemalla
jännenelikulmioita, joiden yksi sivu on ympyrän halkaisija, saadaan helposti
lausekkeet kahden kulman summaa ja erotusta vastaavan jänteen pituudelle
samoin kuin puolta kulmaa vastaavan jänteen pituudelle.
.
Tarkastelemalla
jännenelikulmioita, joiden yksi sivu on ympyrän halkaisija, saadaan helposti
lausekkeet kahden kulman summaa ja erotusta vastaavan jänteen pituudelle
samoin kuin puolta kulmaa vastaavan jänteen pituudelle. ![]() :een ja
:een ja
![]() :een kulmia vastaavat jänteet voidaan laskea geometrisesti, ja
erotusten sekä puolitusten kautta saadaan
:een kulmia vastaavat jänteet voidaan laskea geometrisesti, ja
erotusten sekä puolitusten kautta saadaan ![]() :een,
:een, ![]() :een,
:een,
![]() :een,
:een, ![]() :een, 90':n ja 45':n kulmia vastaavat jänteet.
Yksinkertainen approksimointi, joka perustuu siihen, että pieniä kulmia
vastaavat jänteet suhtautuvat suunnilleen kuten kulmat, johtaa sitten
:een, 90':n ja 45':n kulmia vastaavat jänteet.
Yksinkertainen approksimointi, joka perustuu siihen, että pieniä kulmia
vastaavat jänteet suhtautuvat suunnilleen kuten kulmat, johtaa sitten
![]() :een kulman jänteeseen ja puolitus 30':n kulman jänteeseen.
Kulmien yhteenlaskukaavan avulla saadaan kaikki muut jänteen puolen asteen
välein.
:een kulman jänteeseen ja puolitus 30':n kulman jänteeseen.
Kulmien yhteenlaskukaavan avulla saadaan kaikki muut jänteen puolen asteen
välein.
Tähtitieteen tarpeita palveli myös pallotrigonometria,
jonka systemaattisen esityksen kirjoitti
Menelaos (noin 100
jKr.). Kreikkalaisten trigonometria ei tuntenut meidän ''trigonometrisia
funktioitamme''; kolmioiden ja pallokolmioiden ratkaisut esitettiin puhtaasti
geometrian keinoin. Menelaoksen aikalainen
Heron (noin 75 jKr.)
kirjoitti kuvioiden pinta-aloista ja tilavuuksista. Kolmion alan S sivujen
ja piirin puolikkaan p avulla ilmaisevan Heronin kaavan
Alkuun - Etusivu - Edellinen - Seuraava