Renessanssin (''uudelleensyntymisen'') kiinnostus antiikkiin innosti edelleen myös antiikin matemaattisten klassikkojen käännöksiin. Kaupan tarpeet ja uusi tekniikka, kirjapainotaito, synnyttivät entistä paljon laajalevikkisemmän matemaattisen kirjallisuuden, laskuopit. Renessanssin aikana tehtiin ensimmäiset todella antiikin matematiikkaa pitemmälle menevät uudet keksinnöt, nimenomaan algebran alalla.
Keskiajan lopulla Euroopan matematiikan painopiste oli yliopistojen ulkopuolella. Tosin Pariisin yliopistossa oli vuodesta 1336 voimassa sääntö, jonka mukaan tutkintoa ei myönnetty muuta kuin niille opiskelijoille, jotka valaehtoisesti tunnustivat kuunnelleensa Eukleideen Alkeiden ensimmäisiä kirjoja koskeneita luentoja.
Yleensä itseoppineet laskumestarit levittivät tietoa käytännön elämään kuten kauppaan, kirjanpitoon ja merenkulkuun liittyvästä aritmetiikasta ja algebrasta. Kirjapainotaidon keksiminen 1400-luvun keskivaiheilla ei välittömästi merkinnyt kovin suurta mullistusta matematiikassa. 1400-luvun merkittävin matemaatikko, saksalainen Johannes Müller alias Regiomontanus (1436-76) tosin omisti Nürnbergissä kirjapainon, mutta ennenaikainen kuolema esti häntä toteuttamasta laajoja suunnitelmiaan kääntää tärkeimmät matematiikan klassikkojen teokset suoraan kreikasta latinaksi ja painaa ne. (Konstantinopolin luhistuminen v. 1453 oli saanut monet siellä olleet oppineet siirtymään länteen, ja mukana oli tullut runsaasti kreikkalaisia käsikirjoituksia.) Regiomontanuksen omista töistä on tärkein De triangulis omnimodis, ensimmäinen eurooppalainen systemaattinen trigonometrian esitys. Se ilmestyi painosta vasta 1533. Sisällöltään se vastaa nykyistä trigonometrian peruskurssia, mutta esitys on täysin verbaalista. Nykyistä merkintätapaa ei vielä ollut. Itse sana trigonometria tuli käyttöön vasta 1500-luvun jälkipuoliskolla.
Kirjapainotaito teki 1400-luvun loppupuolella
mahdolliseksi tuottaa lisääntyneen kaupan tarpeisiin
kirjoitettuja laskuoppeja: ensimmäinen tällainen oli anonyymin
tekijän Trevison aritmetiikka vuodelta 1478. Saksassa
vaikuttanut laskuoppien kirjoittaja Adam Riese
(1492-1559) on jättänyt saksan kieleen täsmällisyyttä
ilmentävän puheenparren nach Adam Riese (vrt. ''Elon
laskuopin mukaan''). Hiukan edistyneempiä aritmetiikan
oppikirjoja kirjoittivat mm. italialainen
Luca Pacioli
(1445[?]-1509[?]) ja ranskalainen
Nicolas Chuquet.
Paciolin laajalle levinnyt teos Summa de aritmetica ei
juuri sisältänyt enempää kuin Fibonaccin 300 vuotta
vanhempi kirja. Chuquetin (ranskankielinen!) käsikirjoitus
Triparty en la science des nombres (1484) sisälsi alkeellista
symbolien käyttöä (esim.
![]() esiintyy
muodossa
esiintyy
muodossa
![]() ;
yhteen- ja
vähennyslaskun merkkeinä käytettiin melko yleisesti
kirjaimia p (plus = enemmän) ja m (minus = vähemmän),
käsitteli negatiivisia lukuja ja esitteli ensi kertaa suurten
lukujen nimitykset biljoona, triljoona jne.
Nykyaikaisia piirteitä alkoi yleisemminkin tulla esiin:
1500-luvun alkupuolen laskuopeista löytyy hajanaisia plus- ja
miinusmerkkien sekä yhtäläisyysmerkkien esiintymiä
(=-merkin ensimmäinen käyttäjä, englantilainen
Robert Recorde,
1520-58, perusteli kahden vaakasuoran viivan valintaa
vanhanaikaisella englannilla ''bicause noe .2. thynges can be
moare equalle''), negatiivisia kertoimia, juurimerkkejä jne.
+-merkki on luultavasti muotoutunut
;
yhteen- ja
vähennyslaskun merkkeinä käytettiin melko yleisesti
kirjaimia p (plus = enemmän) ja m (minus = vähemmän),
käsitteli negatiivisia lukuja ja esitteli ensi kertaa suurten
lukujen nimitykset biljoona, triljoona jne.
Nykyaikaisia piirteitä alkoi yleisemminkin tulla esiin:
1500-luvun alkupuolen laskuopeista löytyy hajanaisia plus- ja
miinusmerkkien sekä yhtäläisyysmerkkien esiintymiä
(=-merkin ensimmäinen käyttäjä, englantilainen
Robert Recorde,
1520-58, perusteli kahden vaakasuoran viivan valintaa
vanhanaikaisella englannilla ''bicause noe .2. thynges can be
moare equalle''), negatiivisia kertoimia, juurimerkkejä jne.
+-merkki on luultavasti muotoutunut ![]() -symbolista, - saattaa
olla m-kirjaimen korruptoitunut muoto. Ensi kerran nämä
merkit ovat nykyisessä käytössä
Johann Widmanin
(s. n. 1460) vuonna 1489 ilmestyneessä laskuopissa. Nykyinen
juurimerkkimme on itse asiassa r-kirjaimesta muodostunut; r on
sanan radix alkukirjain; samaa etymologiaa on esim.
retiisi. Se ilmestyi ensi kerran saksalaisen
Christoff Rudolffin
algebran oppikirjassa vuonna 1525.
-symbolista, - saattaa
olla m-kirjaimen korruptoitunut muoto. Ensi kerran nämä
merkit ovat nykyisessä käytössä
Johann Widmanin
(s. n. 1460) vuonna 1489 ilmestyneessä laskuopissa. Nykyinen
juurimerkkimme on itse asiassa r-kirjaimesta muodostunut; r on
sanan radix alkukirjain; samaa etymologiaa on esim.
retiisi. Se ilmestyi ensi kerran saksalaisen
Christoff Rudolffin
algebran oppikirjassa vuonna 1525.
Renessanssin matematiikasta puhuttaessa ei sovi unohtaa
taiteen ja geometrian, etenkin avaruusgeometrian yhteyksiä.
Perspektiivin vähittäinen tulo maalaustaiteeseen todistaa
taiteilijoiden kiinnostuksesta geometriaan. Renessanssin suurista
taiteilijoista esimerkiksi
Albrecht Drer (1471-1528) ja
Leonardo da Vinci
(1452-1519) olivat myös kelpo
matemaatikoita. Drerin 1514 valmistuneessa
Melancholia-kuparipiirroksessa esiintyy ensimmäisiä kertoja
länsimailla taikaneliö, joita etenkin kiinalaiset
olivat konstruoineet jo ainakin ajanlaskun ensimmäisillä
vuosisadoilla. Drerin neliö on
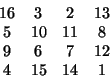
Aikaisemmat aritmetiikan ja algebran oppikirjat jätti varjoon italialaisen lääkärin, matemaatikon ja paavin henkilökohtaisen astrologin Geronimo tai Girolamo Cardanon (1501-76) vuonna 1545 ilmestynyt teos Ars Magna, joka sisälsi raportin ensimmäisistä todella merkittävistä matemaattisista edistysaskeleista sitten antiikin (ars magna = suuri taito tarkoitti algebraa vastakohtana vähempiarvoiselle aritmetiikalle). Kysymyksessä olivat kolmannen ja neljännen asteen yhtälöiden algebralliset ratkaisukaavat. Luca Pacioli oli Omar Khaijamin tavoin pitänyt kolmannen asteen yhtälön ratkaisemista mahdottomana tai ainakin yhtä vaikeana kuin ympyrän neliöinti.
Kertomus ratkaisukaavojen keksimisen ja julkaisun vaiheista kuuluu matematiikan historian värikkäimpiin. - Värikäs oli Cardanon elämäkin, johon sisältyi niin palvelusta astrologina ja lääkärinä Euroopan hoveissa kuin kidustusta inkvisition käsissä ja kirkonkirous Jeesuksen horoskoopin julkaisemisen takia. Säilyttääkseen astrologin maineensa Cardano tiettävästi lakkasi syömästä, kun hänen itselleen ennustamansa kuolinpäivä lähestyi, ja kuolikin sitten oikea-aikaisesti.
Kolmannen asteen yhtälön ratkaisukaavan keksi ilmeisesti Bolognan yliopiston matematiikan professori Scipione del Ferro (1465-1526). Hän ei julkaissut tulostaan, mutta ilmaisi sen kuitenkin oppilaalleen, matemaattisesti keskinkertaiselle Antonio Maria Fiorille. Noin vuonna 1535 oli myös itseoppinut matemaatikko Niccolo Tartaglia (1500[?]-57) keksinyt tai saanut selville ratkaisukaavan. Tartaglian kerskuttua tiedollaan järjestettiin 22. helmikuuta 1535 Fiorin ja Tartaglian kesken julkinen yhtälönratkaisukilpailu. Se päättyi Tartaglian kiistattomaan voittoon, sillä toisin kuin Tartaglia, Fior hallitsi ratkaisukaavan vain yhtä yhtälön kertoimien merkkien kombinaatiota vastaavassa tapauksessa, tapauksessa x3+px=q, mutta ei tapauksessa x3=px+q. Häikäilemätön Cardano onnistui vuonna 1539 perättömien lupausten avulla hankkimaan kaavan Tartaglialta, joka ehdottomasti vaati Cardanoa pitämään tiedon salassa. Tartaglia oli varovasti kätkenyt informaationsa runomuotoon (''Quando che'l cubo con le case appresso/ Se oggualia a qualche numero discreto/ Trovan dui altri, differenti in esso/ ...''), mutta Cardano pääsi siitä selville. Kun kaavat piakkoin tulivat julki Ars Magnassa, syntyi kiivas riita, jonka yhteydessä Cardano syytti Tartaglian itse asiassa varastaneen Ferron kaavan.
Cardanoa tuki syntyneessä polemiikissa hänen
oppilaansa Luigi Ferrari
(1522-65). Cardanolta oli joskus
kysytty ratkaisua ongelmaan, joka johti neljännen asteen
yhtälöön. Cardano ei osannut tehtävää ratkaista, mutta
hän pani Ferrarin tutkimaan asiaa. Tämä keksikin
ratkaisumenetelmän (jonka eräässä vaiheessa on osattava
ratkaista kolmannen asteen yhtälö), ja myös sen Cardano
julkaisi Ars Magnassa. - Cardano ei pyrkinyt väittämään
kolmannen ja neljännen asteen yhtälöiden ratkaisukaavoja
omikseen, vaan tunnusti asianmukaisesti niiden alkuperän.
Kolmannen asteen yhtälön ratkaisukaavoja kutsutaan silti yhä
Cardanon kaavoiksi, neljännen asteen yhtälön
ratkaisukaavoja taas Ferrarin kaavoiksi. - Cardanon nimi
elää myös tekniikassa: kardaaninivel on nimetty hänen
mukaansa.
Cardanon kaavojen johtamiseksi tarkastellaan kolmannen
asteen yhtälöä muodossa
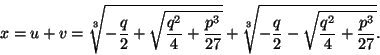
Ferrarin kaavoihin päästään muotoa
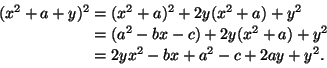
Kolmannen ja neljännen asteen yhtälöiden ratkaisukaavojen keksimisen suurin merkitys lienee siinä, että nyt saatettiin havaita uutta löydettävää vielä olevan jäljellä. Antiikin viisaat eivät olleet vielä rakentaneet matematiikkaa valmiiksi. Cardanon ja Ferrarin kaavat eivät sinänsä ole kovin hyödyllisiä: käytännössä kolmannen ja neljännen asteen yhtälöiden ratkaisut haetaan approksimaatioista, kuten oli osattu tehdä jo Cardanon aikanakin.
Cardanon kaavat johtavat silloin, kun yhtälön kaikki kolme juurta ovat reaalisia, tilanteeseen, jossa reaalijuuret esiintyvät kahden kompleksiluvun, itse asiassa kahden liittokompleksiluvun kuutiojuurten erotuksina. Tämä ns. casus irreducibilis jäi Cardanolle epäselväksi, vaikka hän siihen huomiota kiinnittikin. (Kompleksilukuja käyttävä nykymatemaatikko selvittää ongelman helposti.)
Cardano käsitteli negatiivisten lukujen neliöjuuria
toisen asteen yhtälön tapauksessa (''jaa luku 10 kahteen osaan,
joiden tulo on 40''), mutta vähän myöhemmin
Raffael Bombelli
(1526[?]-73) huomasi eräissä konkreettisissa
tapauksissa kuten yhtälössä
x3=15x + 4, jolla on ilmeinen
ratkaisu x=4 ja Cardanon kaavojen mukainen ratkaisu
![]() ,
että jos
''liittoluvuista'' otetut kuutiojuuret oletetaan toistensa
''liittoluvuiksi'', kaavat toimivat sellaisinaan. Bombelli otti
käyttöön nimitykset piu di meno ja meno di
meno, jotka vastaavat nykymerkintöjä i ja -i, ja
näille mm. kaavoja
,
että jos
''liittoluvuista'' otetut kuutiojuuret oletetaan toistensa
''liittoluvuiksi'', kaavat toimivat sellaisinaan. Bombelli otti
käyttöön nimitykset piu di meno ja meno di
meno, jotka vastaavat nykymerkintöjä i ja -i, ja
näille mm. kaavoja
![]() vastaavat
laskusäännöt. Jos
vastaavat
laskusäännöt. Jos
![]() ,
niin
a3-3ab2=2 ja
,
niin
a3-3ab2=2 ja
![]() .
Näistä nähdään, että voidaan kirjoittaa
.
Näistä nähdään, että voidaan kirjoittaa
![]() ja edelleen
ja edelleen
![]() .
Kun tästä ratkaistu a2 sijoitetaan
yhtälöön
3a2b-b3=11, saadaan
15b-4b3=11. Nyt b=1 ja
a=2. Cardanon kaavan kahden kolmannen juuren summa on todellakin
2a=4.
.
Kun tästä ratkaistu a2 sijoitetaan
yhtälöön
3a2b-b3=11, saadaan
15b-4b3=11. Nyt b=1 ja
a=2. Cardanon kaavan kahden kolmannen juuren summa on todellakin
2a=4.
Bombellin Algebra ilmestyi v. 1572. Imaginaarilukujen todellinen luonne selvisi kuitenkin vasta vähitellen seuraavien kolmen vuosisadan kuluessa.
Kolmannen ja neljännen asteen yhtälöiden ratkaisun ydin on tehtävän palauttamisessa alemmanasteisen yhtälön, resolventtiyhtälön, ratkaisemiseen. Ikävä kyllä viidennen ja korkeamman asteen yhtälöiden tapauksessa vastaavalla tavalla konstruoidut resolventtiyhtälöt tulevat olemaan korkeampaa astetta kuin alkuperäinen yhtälö.
1500-luvun lopun merkittävin ja monipuolisin matemaatikko oli ranskalainen juristi ja hallintomies Francois Viète eli Vieta (1540-1603). Viète teki palveluksia Ranskan hallitsijoille mm. salakirjoituksia selvittämällä; espanjalaisten käyttämän salakirjoituksen avaaminen oli näille niin yllättävää, että kuningas Filip II syytti ranskalaisia mustaan magiaan turvautumisesta.
Viète oli flaamilaissyntyisen, mutta enimmäkseen
Hollannissa toimineen insinöörin
Simon Stevinin
(1548-1620) ohella innokkaimpia desimaalilukujen käytön
puoltajia. Tarkoissa laskutoimituksissa käytettiin tuolloin
yhä babylonialais - hellenistisen tradition mukaisesti
seksagesimaalimurtolukuja. Desimaalimerkintä ei heti vakiintunut
nykyiselleen. Viètellä esiintyi mm. merkintöjä
Kauaskantoisin Vièten uudistuksista oli kirjainten käyttö tunnettujen ja tuntemattomien suureiden merkinnässä. Kirjassaan In artem analyticem isagoge (Johdatus analyysin taitoon, 1591) Viète merkitsi vokaaleilla tuntemattomia suureita ja konsonanteilla tunnettuja. Aivan täysin nykyaikaisia eivät Vièten käyttämät symbolit kuitenkaan vielä olleet: osa kaavoissa tarvittavista merkinnöistä oli sanallisia. Esimerkiksi yhtälön A3+BA=CA2+D Viète kirjoitti ''A cub + B plano in A æ quatur C in A quad + D solido''. Vièten eri aikalaisten kirjoituksissa esiintyvät yhteensä jokseenkin kaikki nykyiset symbolit, mutta yhtä aikaa ne tulivat käyttöön vasta seuraavan vuosisadan puolella
Algebrassa Viète havaitsi osan yhtälöiden juurien ja kertoimien välisistä yhteyksistä (kuten että juurien summan vastaluku on lähinnä korkeimman tuntemattoman potenssin kerroin), mutta koska hän hyväksyi vain positiiviset juuret, teoria jäi vaillinaiseksi. Polynomiyhtälön kertoimet juurien avulla lausuvia kaavoja kutsutaan edelleen Vièten kaavoiksi.
Kolmannen asteen yhtälön
x3+px+q=0 Viète
ratkaisi sijoituksella
Trigonometriaa Viète edisti mm. tyyppiä
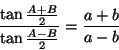
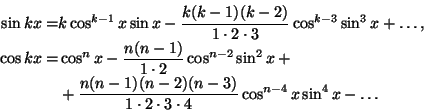
Viète osasi valjastaa trigonometrian algebran
palvelukseen: hän johti trigonometriseen sijoitukseen perustuvan
kolmannen asteen yhtälön ratkaisukaavan: mielivaltaiselle
kulmalle ![]() pätee
pätee
Kuuluisaksi tuli Vièten antama yllättävä
trigonometrinen ratkaisu flaamilaisen
Adriaen van Roomenin (1561-1615)
esittämälle 45. asteen yhtälölle.
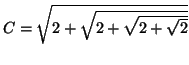 .
Viete tunnisti, että yhtälön vasen puoli on
.
Viete tunnisti, että yhtälön vasen puoli on
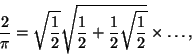
Astronomia ja merenkulku tarvitsevat varsin mutkikkaita
trigonometrisia numerolaskuja. Pitkien kertolaskujen muuttamiseksi
helpommiksi yhteen- ja vähennyslaskuiksi kehittyi 1500-luvulla,
löytöretkien vuosisadalla, ns.
prostafairesis-menetelmä. Se perustui tyyppiä
Originelli skotlantilainen tilanomistaja, Merchistonin paroni
John Napier (Neper) (1550-1617) (jonka
julkaisutuotantoon kuuluu mm. aikanaan tavattoman suuren levikin
saanut numerologinen todistus sille, että paavi on Antikristus,
mutta myös käyttökelpoisia pallotrigonometrian kaavoja)
keksi lyhemmän tavan. Jos tarkastelee geometrisen jonon
termejä, huomaa, että jonon kahden termin tulo esiintyy
jonossa paikalla, jonka järjestysnumero saadaan laskemalla
yhteen alkuperäisten termien järjestysluvut. Napier keksi
ottaa käyttöön jonon, jonka termit ovat hyvin lähellä
toisiaan. Tällaisen jonon hän sai valitsemalla suhdeluvuksi
luvun
![]() .
Desimaalien välttämiseksi
Napier kertoi jonon luvut luvulla 107. Lukua N vastaava
Napierin logaritmi
.
Desimaalien välttämiseksi
Napier kertoi jonon luvut luvulla 107. Lukua N vastaava
Napierin logaritmi
![]() on siten luku, jolle
pätee
on siten luku, jolle
pätee
Logaritmitaulukkojensa luvut Napier laski geometrisista
sarjoista monimutkaisella interpolaatiomenettelyllä.
Ensimmäisessä vaiheessa Napier vähensi luvusta 10000000 sen
kymmenesmiljoonasosan, erotuksesta jälleen kymmenesmiljoonasosan
jne., kunnes sadan vähennyksen jälkeen tullaan lukuun
9999900,000495. Tämän luvun Napier-logaritmi on 100.
Lineaarinen ekstrapolaatio näyttää, että luvun 9999900
Napier-logaritmi on 100,000495. Tämän jälkeen Napier alkaa
vähentää luvusta 10000000 sen sadastuhannesosan, erotuksesta
samoin jne. Erotukset ovat jälleen geometrisen jonon lukuja, ja
niiden Napier-logaritmit 100,000495:n monikertoja. 50:n
vähennyksen jälkeen ollaan luvussa 9995001,224804 (Napier teki
tässä kolmanteen desimaaliin vaikuttavan laskuvirheen), jonka
Napier-logaritmi on
![]() .
Ekstrapolointi antaa luvun 9995000 Napier-logaritmiksi
5001,250175. Nyt Napier rakentaa vielä 21-rivisen ja
69-sarakkeisen taulukon, jossa kukin luku on yllä oleva luku
vähennettynä kahdestuhannesosallaan ja samalla vasemmalla
oleva luku vähennettynä sadasosallaan. Tällöin kunkin
sarakkeen alin luku on suunnilleen sama kuin seuraavan sarakkeen
ylin luku ja taulukon oikeaan alakulmaan tulee luku 4998609,4019.
Kun vielä ekstrapoloidaan luvun 9900000 Napier-logaritmiksi
taulukon vasemmanpuoleisen sarakkeen avulla (jonka
Napier-logaritmit ovat 5001,250175:n monikertoja) 100503,223,
saadaan p:nnellä rivillä ja q:nnessa sarakkeessa olevan
luvun Napier-logaritmiksi
.
Ekstrapolointi antaa luvun 9995000 Napier-logaritmiksi
5001,250175. Nyt Napier rakentaa vielä 21-rivisen ja
69-sarakkeisen taulukon, jossa kukin luku on yllä oleva luku
vähennettynä kahdestuhannesosallaan ja samalla vasemmalla
oleva luku vähennettynä sadasosallaan. Tällöin kunkin
sarakkeen alin luku on suunnilleen sama kuin seuraavan sarakkeen
ylin luku ja taulukon oikeaan alakulmaan tulee luku 4998609,4019.
Kun vielä ekstrapoloidaan luvun 9900000 Napier-logaritmiksi
taulukon vasemmanpuoleisen sarakkeen avulla (jonka
Napier-logaritmit ovat 5001,250175:n monikertoja) 100503,223,
saadaan p:nnellä rivillä ja q:nnessa sarakkeessa olevan
luvun Napier-logaritmiksi
![]() .
- Koska Napier tähtäsi itse asiassa kulmien
sinien logaritmeihin ja hänen kehyksenään oli suorakulmainen
kolmio, jonka hypotenuusa on 107, kuvailtu prosessi antoi
mahdollisuuden laskea sinien logaritmit
.
- Koska Napier tähtäsi itse asiassa kulmien
sinien logaritmeihin ja hänen kehyksenään oli suorakulmainen
kolmio, jonka hypotenuusa on 107, kuvailtu prosessi antoi
mahdollisuuden laskea sinien logaritmit
![]() :n ja
:n ja
![]() :n väliltä. Pienempiin kulmiin pääsee
käsiksi kaavan
:n väliltä. Pienempiin kulmiin pääsee
käsiksi kaavan
![]() avulla.
avulla.
Napier perusteli menetelmäänsä
geometris-dynaamisella tarkastelulla. Jos piste D liikkuu
tasaisella nopeudella 107 pitkin puolisuoraa ![]() ja piste
C liikkuu pitkin janaa AB, jonka pituus on 107 niin, että
sen nopeus jokaisella ajan hetkellä on CB, ja jos x=OD,
y=CB, niin ajan t funktiona on x=107t ja y'=-y,
ja piste
C liikkuu pitkin janaa AB, jonka pituus on 107 niin, että
sen nopeus jokaisella ajan hetkellä on CB, ja jos x=OD,
y=CB, niin ajan t funktiona on x=107t ja y'=-y,
![]() ,
,
![]() .
Tästä saadaan
.
Tästä saadaan
![]() .
Interpolaatio-approksimaation takia
Napierin logaritmit eivät olleet aivan tasan edellisen kaavan
mukaisia.
.
Interpolaatio-approksimaation takia
Napierin logaritmit eivät olleet aivan tasan edellisen kaavan
mukaisia.
Kreikan sanoista logos 'suhde' ja arithmos 'luku' kokoon pantu sana logaritmi on Napierin käyttöön ottama, samoin kuin pilkun tai pisteen käyttö desimaalierottimena. Aluksi Napier oli kutsunut näitä lukuja keinotekoisiksi luvuiksi.
Napier julkaisi ideansa ja logaritmitaulukkonsa 1614
teoksessa Mirifici logarithorum canon descriptio ensi
sijassa helpottamaan trigonometrisia laskuja. Lukujen logaritmien
sijasta hän puhuikin sinien logaritmeista. Seuraavana vuonna
lontoolainen professori (ilmeisesti ensimmäinen matematiikan
professori Englannissa) Henry Briggs (1561-1639)
kiinnostui logaritmeista. Hän vieraili Napierin luona
Skotlannissa, ja yhteisymmärryksessä Napier ja Briggs
päätyivät muunnettuun järjestelmään, jossa kantalukuna
olisi 10. Briggs julkaisi 1624 lukujen 1 - 20![]() 000 ja
90
000 ja
90![]() 000 - 100
000 - 100![]() 000 14-desimaaliset 10-kantaiset
logaritmitaulut. Briggsin taulukko perustui lukujen
000 14-desimaaliset 10-kantaiset
logaritmitaulut. Briggsin taulukko perustui lukujen
![]() ,
101/4, 101/8, ...,
101/254 laskemiseen
peräkkäisillä neliöjuurenotoilla. Logaritmit levisivät
yleiseen käyttöön hämmästyttävän nopeasti. Keplerin
mielestä logaritmit pidensivät taähtitieteilijän iän
kaksinkertaiseksi.
,
101/4, 101/8, ...,
101/254 laskemiseen
peräkkäisillä neliöjuurenotoilla. Logaritmit levisivät
yleiseen käyttöön hämmästyttävän nopeasti. Keplerin
mielestä logaritmit pidensivät taähtitieteilijän iän
kaksinkertaiseksi.
Napierin ja Briggsin rinnalla kunnia logaritmien keksimisestä kuuluu myös sveitsiläiselle kojeiden rakentajalle Jobst Bürgille (1552-1632), jonka itsenäisesti jo 1588 keksimä logaritmikäsite tuli julkisuuteen vasta 1620. Bürgin logaritmit perustuivat luvun 1,0001 potensseihin: luvun 108(1+10-4)n Bürgin logaritmi on 10n.
Myös luonnolliset logaritmit, siis kantalukuun eperustuvat, ilmaantuivat matematiikkaan vuoden 1620 paikkeilla, vaikka niiden tärkeys havaittiinkin vasta myöhemmin, differentiaali- ja integraalilaskennan kehityttyä tarpeeksi.
Logaritmien yhteys matemaattiseen analyysiin alkaa
belgialaisen jesuiitan
Gregóire de San Vincentin vuoden
1620 paikkeilla tekemästä havainnosta, jonka mukaan (taas
nykyaikaistetun puhetavan mukaan) suorakulmaisen hyperbelin
xy=1, x-akselin ja suorien x=a,
x=b rajaaman alueen ala on sama kuin hyperbelin,
x-akselin ja suorien x=ta ja x=tb
rajaaman alueen. Asian toteaa helposti approksimoimalla alueita
esim. n:n suorakaiteen muodostamilla porraskuvioilla: edellisen
alueen tapauksessa i:nnen suorakaiteen korkeus on t kertaa
jälkimmäisen alueen vastaavan suorakaiteen korkeus, kun taas
jälkimmäisessä tapauksessa suorakaiteiden kannat ovat tkertaa edellisen tapauksen suorakaiteiden kannat. Tästä
seuraa, että hyperbelin määrittämällä pinta-alalla on
logaritminen yhteenlaskuominaisuus - sittemmin onkin selvinnyt,
että kuvattu ala on
![]() .
.
Alkuun - Etusivu - Edellinen - Seuraava