otsikkokuva

Miksi $\pi$ on irrationaalinen?

Matti Lehtinen

Selailin erästä hiljattain ilmestynyttä lukion lyhyen matematiikan oppikirjaa. Siinä käsiteltiin, niin kuin oikein ja kohtuullista on, erityyppisiä lukuja. Irrationaaliluvuista ensimmäisenä esimerkkinä oli ''kuuluisin irrationaaliluku'' $\pi=3{,}14145926\dots$ . Kirja ei kerro, miksi $\pi$ , ympyrän kehän ja halkaisijan pituuksien suhde, on irrationaalinen. Eipä tietoa löydy muistakaan oppikirjoista. Kaikki me kuitenkin pidämme asiaa tunnettuna ja selvänä. Mutta eihän matematiikassa saa luottaa kuulopuheisiin, väitteet on perusteltava!

Irrationaalilukuja on

Reaaliluvut ovat joko rationaalisia, kokonaislukujen osamääriä $\frac{p}{q}$ , $q\neq 0$ , tai sitten ei. Reaaliluvut, jotka eivät ole rationaalisia, ovat irrationaalisia. Jo lähes 2500 vuotta sitten kreikkalaisen kulttuurin piirissä tehtiin se merkittävä ja matematiikan kehitykseen syvällisesti vaikuttanut havainto, että muutamat janojen pituuksien suhteet kuten neliön sivun ja lävistäjän pituuksien suhde tai säännöllisen viisikulmion sivun ja lävistäjän pituuksien suhde eivät ole ilmaistavissa kokonaislukujen suhteena, toisin sanoen ne ovat irrationaalisia. Irrationaalisuustodistukset ovat epäsuoria: jos neliön sivu olisi 1 ja sen lävistäjän ja sivun suhde olisi $\frac{p}{q}$ , ja p:llä ja q:lla ei olisi yhteisiä tekijöitä (sellaisethan voidaan aina supistaa murtoluvusta pois), niin Pythagoraan lauseen mukaan olisi

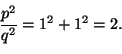
$\begin{displaymath}\frac{p^2}{q^2}=1^2+1^2=2. \end{displaymath}$

Tällöin olisi p²=2q². Mutta nyt p olisi parillinen, p=2s, ja saataisiin 4s²=2q², q²=2s². Siis q:kin olisi parillinen, ja p:llä ja q:lla olisikin yhteinen tekijä 2.

Irrationaalilukuja on paljon

Irrationaalilukuja on siis olemassa. Itse asiassa niitä on kovin paljonkin. Umpimähkään valittu reaaliluku on melkoisella varmuudella irrationaalinen. Rationaalilukujen joukko on nimittäin numeroituva. Jokaiselle rationaaliluvulle voidaan antaa ikioma järjestysnumero luonnollisten lukujen joukosta. Itse asiassa tullaan toimeen vain näennäisesti pienellä osalla kaikista luonnollisista luvuista. Jokainen rationaaliluku r voidaan kirjoittaa yksikäsitteisesti muotoon

$\begin{displaymath}r=(-1)^k\frac{p}{q}, \end{displaymath}$

missä k=0 tai k=1, p on luonnollinen luku (0 on mukana) ja q nollasta eroava luonnollinen luku, jolla ei ole yhteisiä tekijöitä p:n kanssa. Jos p=0, kiinnitetään vielä q=1. Nyt jokaiseen rationaalilukuun r voidaan liittää esimerkiksi luonnollinen luku f(r)=2^k3^p5^q. Kahteen eri rationaalilukuun tulee näin aina liitetyksi eri luonnollinen luku.

Väitetty rationaalilukujen ''harvalukuisuus'' seuraa edellisestä. Otetaan mikä hyvänsä positiivinen luku a, kuinka läheltä nollaa tahansa. Ympäröidään jokainen rationaaliluku r janalla, jonka pituus on $\frac{a}{2^{f(r)}}$ . Näiden janojen yhteinen pituus on varmasti enintään

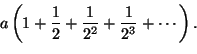
$\begin{displaymath}a\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots\right). \end{displaymath}$

Mutta geometrisen sarjan summakaavan mukaan summa on sama kuin

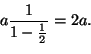
$\begin{displaymath}a\frac{1}{1-\frac{1}{2}}=2a. \end{displaymath}$

Kaikki rationaaliluvut voidaan siis lukusuoralla eristää sellaiseen osaan, jonka pituus voidaan (a:n valinnalla) saada miten pieneksi tahansa. Kaikki, mitä yli jää, on irrationaalilukujen aluetta. (Asia ei tietenkään ole kovin havainnollinen. Rationaalilukuja on toisaalta tiheässä; esimerkiksi jokainen lukusuoran jana, miten lyhyt tahansa, sisältää äärettömän monta rationaalilukua.)

Mutta onko $\pi$ irrationaalinen?

Vaikka irrationaaliluvut näyttävätkin muodostavan lukujen enemmistön, yksittäisen luvun irrationaalisuus ei yleensä ole helppo osoittaa. Lukua $\pi$ (merkintä on peräisin 1700-luvulta) ounasteltiin irrationaaliseksi jo antiikin aikoina. Ensimmäisen, joskin hiukan aukkoisen todistuksen asialle on kuitenkin julkaissut sveitsiläinen Johann Heinrich Lambert vuonna 1766. Lambert johti tangenttifunktiolle ketjumurtolukuesityksen ja päätteli sen perusteella, että jos x on rationaalinen, $\tan x$ on irrationaalinen. Koska $\tan\frac{\pi}{4}=1$ , $\frac{\pi}{4}$ ja siten myös $\pi$ on irrationaalinen.

Seuraavaa $\pi$ :n irrationaalisuustodistusta pidetään nykyisin yksinkertaisimpana. Se on koulutiedoin ymmärrettävissä, mutta on silti melko monipolvinen. Tämän todistuksen ajatuksen esittivät amerikkalainen I. Niven ja japanilainen Y. Iwamoto 1940-luvun lopulla.

Todistetaan itse asiassa vähän enemmän kuin $\pi$ :n irrationaalisuus, nimittäin, että luku $\pi^2$ on irrationaalinen. Tämä riittää itse $\pi$ :nkin irrationaaliseksi todistamiseen, koska rationaaliluvun neliö tietenkin on rationaalinen.

Muutamia polynomeja ja niiden derivaattoja

Lähdetään liikkeelle astetta 2n olevista polynomeista

$\begin{displaymath}p_n(x)=\frac{1}{n!}x^n(1-x)^n,\quad n\ge 1. \end{displaymath}$

On ilmeistä, että

$\begin{displaymath} 0<p_n(x)<\frac{1}{n!},\quad \text{kun}\ 0<x<1. \end{displaymath}$

(1)

Väitämme, että polynomien p_n kaikkien kertalukujen derivaatat saavat pisteissä 0 ja 1 kokonaislukuarvon. Tämä nähdään oikeaksi induktiopäättelyn avulla. Ensiksikin p₁(x)=x(1-x)=x-x², joten p₁'(x)=1-2x, p₁''(x)=-2 ja p₁:n korkeammat derivaatat p₁^(k)(x), k>2, ovat nollia. Väite on siis tosi, kun n=1. Tehdään sitten sellainen induktio-oletus, että polynomien p₁(x), ..., p_n-1(x) kaikkien kertalukujen derivaatat saavat pisteissä 0 ja 1 kokonaislukuarvon. Nyt

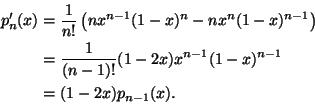
$\begin{displaymath}\begin{split} p_n'(x)&=\frac{1}{n!}\left(nx^{n-1}(1-x)^n-nx^n... ...1)!}(1-2x)x^{n-1}(1-x)^{n-1}\\ &=(1-2x)p_{n-1}(x). \end{split}\end{displaymath}$

Tulon derivaattakaavaa toistuvasti soveltaen näemme, että p_n(x):n kaikkien kertalukujen derivaatat ovat x:n ja polynomien p_j(x), $j\le n-1$ , derivaattojen polynomeja. Induktio-oletuksesta seuraa, että kyseiset derivaatat saavat 0:ssa ja 1:ssä vain kokonaislukuarvoja.

Muodostetaan nyt polynomin p_n derivaatoista ja luvusta $\pi$ seuraavanlainen polynomi:

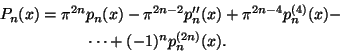
$\begin{displaymath}\begin{split} P_n(x)= \pi^{2n} &p_n(x)-\pi^{2n- 2}p_n''(x)+\pi^{2n-4}p_n^{(4)}(x)-\\ &\cdots+(-1)^np_n^{(2n)}(x). \end{split}\end{displaymath}$

P_n(x):n lauseke on pantu kokoon tarkoitushakuisesti. Ensinnäkin havaitaan, että p_n:n ne derivaatat, joiden kertaluku on suurempi kuin 2n, ovat nollia, onhan p_n(x) polynomi, jonka aste on 2n. Edelleen

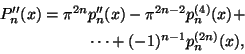
$\begin{displaymath}\begin{split} P_n''(x)= \pi^{2n} &p_n''(x)-\pi^{2n-2}p_n^{(4)}(x)+\\ &\cdots+(-1)^{n- 1}p_n^{(2n)}(x), \end{split}\end{displaymath}$

joten

$\begin{displaymath}\pi^2P_n(x)+P_n''(x)=\pi^{2n+2}p_n(x). \end{displaymath}$

Muodostetaan nyt tulon derivointikaavan avulla funktion

$\begin{displaymath}f(x)=P_n'(x)\sin(\pi x)-\pi P_n(x)\cos(\pi x) \end{displaymath}$

derivaatta f'(x):

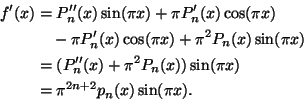
$\begin{displaymath}\begin{split} f'(x)&=P_n''(x)\sin(\pi x)+\pi P_n'(x)\cos(\pi ... ..._n(x))\sin(\pi x)\\ &=\pi^{2n+2}p_n(x)\sin(\pi x). \end{split}\end{displaymath}$

Mihin tätä tarvitaan? Se näyttää meille, että

$\begin{displaymath} \begin{split} \int\nolimits_0^1\pi^{2n+2} &p_n(x)\sin(\pi x)\,dx=\Big\vert^1_0f(x)\\ &=\pi(P_n(1)+P_n(0)). \end{split}\end{displaymath}$

(2)

Lopullinen hyökkäys

Tehdään nyt ratkaiseva vastaoletus. Oletamme, että

$\begin{displaymath}\pi^2=\frac{a}{b}, \end{displaymath}$

missä a ja b ovat kokonaislukuja. Koska P_n(x) koostuu $\pi^2$ :sta, enintään potenssiin n korotettuna, ja p_n(x):n derivaatoista, niin P_n(0) ja P_n(1) ovat muotoa $\frac{A}{b^n}$ ja $\frac{B}{b^n}$ , missä A ja B ovat kokonaislukuja. Lisäksi $\pi^{2n+2}=\pi^2\frac{a^n}{b^n}$ ja (2) saa muodon

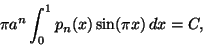
$\begin{displaymath}\pi a^n\int\nolimits_0^1p_n(x)\sin(\pi x)\,dx=C, \end{displaymath}$

missä C on positiivinen kokonaisluku. Mutta kun 0<x<1, niin $0<\sin(\pi x)<1$ . Kun otetaan mukaan epäyhtälö (1), nähdään, että edellisen integraalin integroitava funktio on koko integroimisvälillä positiivinen, mutta arvoltaan pienempi kuin $\frac{1}{n!}$ . Koska integroimisvälin pituus on 1, itse integraali on positiivinen luku, joka on pienempi kuin $\frac{1}{n!}$ . Mutta tämä merkitsee, että

$\begin{displaymath} \pi\frac{a^n}{n!}\ge C, \end{displaymath}$

(3)

riippumatta n:n arvosta. Nyt tarvitsemme vielä yhden matematiikan yleistiedon. Jos a on mielivaltainen luku, niin

$\begin{displaymath} \lim_{n\to\infty}\frac{a^n}{n!}=0. \end{displaymath}$

(4)

Tästä yhtälöstä on helppo vakuuttua vaikkapa ajattelemalla, että osamäärän osoittajassa ja nimittäjässä on molemmissa n tekijää, ja kun n kasvaa, nimittäjään kerääntyy enemmän ja enemmän tekijöitä, jotka ovat >a. Mutta (3) ja (4) ovat ilmeisessä ristiriidassa keskenään. Vastaoletus luvun $\pi^2$ rationaalisuudesta on siis väärä!

Mutta ongelmia vielä jääkin

Irrationaaliluvutkin jakautuvat kahteen luokkaan. Algebralliset luvut ovat jonkin kokonaislukukertoimisen polynomin nollakohtia. Muut irrationaaliluvut ovat transkendenttilukuja. Esimerkiksi $\sqrt 2$ on algebrallinen, koska se on polynomin x²-2 nollakohta. Osoittautuu, että algebrallisiakin irrationaalilukuja on ''vain'' numeroituva määrä, joten ''melkein kaikki'' reaaliluvut ovat transkendenttilukuja. Mutta kysymys yksittäisen luvun transkendenttisuudesta on yleensä vaikea ratkaista. Luku $\pi$ todistettiin transkendenttiluvuksi vuonna 1882. Tämä ratkaisi yli 2000 vuotta pohditun ongelman ympyrän neliöinnistä, geometrisesta konstruktiosta, jolla voitaisiin (harppia ja viivoitinta käyttäen) löytää sellaisen neliön sivu, jonka ala on tunnetun, esimerkiksi yksikkösäteisen, ympyrän ala. Koska geometriset konstruktiot ovat suorien ja ympyröiden leikkauspisteiden etsimisiä ja näiden yhtälöt ovat ensimmäisen ja toisen asteen polynomeja, ei konstruktioilla päästä pisteistä, joiden koordinaatit ovat rationaalilukuja, pisteisiin, joiden koordinaatit ovat transkendenttilukuja. Luvun $\pi$ transkendenttisuus merkitsee, että ''ympyrän neliöintiongelma'' on ratkeamaton. Mutta siihen, miksi $\pi$ on transkendenttinen, emme nyt puutu.

Solmu
2001-05-15

Miksi on irrationaalinen?